Information Technology Reference
In-Depth Information
z
i
2
r
y
= s
inf. saddles
locus
2
n
y
= s
lowest saddle
divergence line
s
2
i
2
n
s
− s
z
n
max locus
max
2
y
= s
sup. saddles
locus
2
y
= s
Figure 5.15
Solution and center locus in the plane
z
n
z
i
for a nongeneric TLS. The dotted
line represents the divergence line.
Hence, the solution is contained in the hyperplane (
nongeneric TLS subspace
)
through the origin and normal to the
A
T
A
eigenvector
v
n
. It confirms the addi-
tional constraint
x
−
⊥
v
n
+
1
.
Furthermore, in every plane
z
n
z
i
the hyperbolas
degenerate in two straight lines given by
z
n
1
(see
Figure 5.15). In every plane
z
n
z
i
the latter straight line is the
divergence straight
line
because it attracts all divergent weight trajectories. Indeed, it represents the
equilevel surfaces center locus for
t
<λ
n
.
=
0and
z
i
=
q
i
/(λ
−
λ
)
i
n
Proposition 120 (Nongeneric TLS Subspace)
The nongeneric TLS subspace
has dimension n
1
, n being the dimension of the TLS hyperplane. In this sub-
space, the lower saddle
(
i.e., the critical point corresponding to
−
σ
n
)
loses its
dimension of escape and then represents a minimum.
The most important consequence of this proposition is the possibility of repeat-
ing exactly all the TLS stability analysis on this lower-dimensional subspace.
Figure 5.15 shows that for every plane
z
n
z
i
the saddle/minimum is always closer
to the asymptote than the other inferior (
t
<λ
i
) saddles. It implies the following
propositions.
Proposition 121 (Null Initial Conditions as Universal Choice)
The origin
is always between the saddle/solution and the maximum. Hence, the choice of



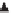










Search WWH ::

Custom Search