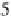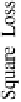Information Technology Reference
In-Depth Information
Fig. 2.1
Square loss as a
function of
y
j
−
f(x
j
)
2.2.1 Subset Ranking with Regression
Cossock and Zhang [
5
] solve the problem of ranking by reducing it to regression.
Given
x
m
j
1
, a set of documents associated with training query
q
, and the
ground truth labels
y
={
x
j
}
=
m
j
=
1
of these documents in terms of multiple ordered
categories, suppose a scoring function
f
is used to rank these documents. The loss
function is defined as the following square loss,
={
y
j
}
x
j
,y
j
)
=
y
j
−
f(x
j
)
2
.
L(f
;
(2.1)
The curve of the square loss is as shown in Fig.
2.1
. From the figure one can
see that if and only if the output of the scoring function
f(x
j
)
exactly equals the
label
y
j
, there is no loss. Otherwise the loss increases in a quadratic order. In other
words, for a relevant document, only if the scoring function can exactly output 1,
there will be zero loss. Otherwise if the output is 2 which seems to be an even
stronger prediction of relevance for this document, there will be some loss. This is,
in some sense, not very reasonable.
As an extension of the above method, an importance weighted regression model
is further studied in [
5
]. The weights help the new model focus more on the regres-
sion error on the relevant documents (which are more likely to appear on top of the
ranking result). Furthermore, the introduction of regularization terms to the regres-
sion loss is also investigated, which aims at making the method more generalizable
(i.e., perform better on unseen test data).
In addition to the proposal of the methods, theoretical analysis on the use of the
square loss function is also performed in [
5
]. The basic conclusion is that the square
loss can upper bound the NDCG-based ranking error (see Chap. 5 for more details).
However, according to the above discussions, even if there is a large regression loss,
the corresponding ranking can still be optimal as long as the relative orders between
the predictions
f(x
j
)
(
j
=
1
,...,m
) are in accordance with those defined by the
ground truth label. As a result, we can expect that the square loss is a loose bound
of the NDCG-based ranking error.