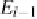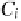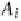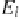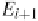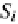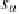Information Technology Reference
In-Depth Information
Fig. 13.3
The DBN model
For a given position
i
, in addition to the observed variable
C
i
indicating whether
there is a click or not at this position, the following hidden binary variables are de-
fined to model examination, perceived relevance, and actual relevance, respectively:
•
E
i
: did the user examine the URL?
•
A
i
: was the user attracted by the URL?
•
S
i
: was the user satisfied by the actual document?
The model in Fig.
13.3
can be mathematically described as below.
A
i
=
1
,
i
=
1
⇔
C
i
=
1
,
P(A
i
=
1
)
=
a
u
,
P(S
i
=
1
|
C
i
=
1
)
=
s
u
,
C
i
=
0
⇒
S
i
=
0
,
(13.11)
S
i
=
1
⇒
E
i
+
1
=
0
,
P(E
i
+
1
=
|
E
i
=
1
,S
i
=
=
1
0
)
γ,
E
i
=
⇒
E
i
+
1
=
0
0
.
A detailed explanation of the model now follows. First one assumes that there is a
click if and only if the user looks at the URL and is attracted by it. The probability of
being attracted depends only on the URL. Second, the user scans the URLs linearly
from top to bottom until he/she decides to stop. After the user clicks and visits the
URL, there is a certain probability that he/she will be satisfied by this URL. On the
other hand, if he/she does not click, he/she will not be satisfied. Once the user is
satisfied by the URL he/she has visited, he/she stops his/her search. If the user is
not satisfied by the current result, there is a probability 1
γ
that the user abandons
his/her search and a probability
γ
that the user examines the next URL. If the user
does not examine the position
i
, he/she will not examine the subsequent positions.
Note that, unlike previous models, the DBN model has two variables
a
u
and
s
u
related to the relevance of the document. The first one models the perceived
−