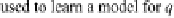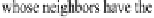Information Technology Reference
In-Depth Information
Fig. 7.1
Illustration of KNN Offline-1
retrieved. Then, a model
h
q
i
is trained using the labeled data in
N
k
(q
i
)
offline and in
advance. In the test process, for a new query
q
, one first finds its
k
nearest neighbors
N
k
(q)
, and then compares
N
k
(q)
with every
N
k
(q
i
)(i
1
,...,n)
so as to find the
one sharing the largest number of instances with
N
k
(q)
. Suppose it is
N
k
(q
i
∗
)
. Then
h
q
i
∗
, the model learned from the selected neighborhood
N
k
(q
i
∗
)
(it has been created
offline and in advance), is used to rank the documents of query
q
.
KNN Offline-2 works as follows (see Fig.
7.2
). First, for each training query
q
i
, its
k
nearest neighbors
N
k
(q
i
)
in the query feature space are retrieved. Then,
a model
h
q
i
is trained using the labeled data in
N
k
(q
i
)
offline and in advance. In-
stead of seeking the
k
nearest neighbors for the test query
q
, one only finds its
single nearest neighbor in the query feature space. Supposing this nearest neigh-
bor to be
q
i
∗
, then the model
h
q
i
∗
trained from
N
k
(q
i
∗
)
is used to test query
q
.In
this way, one further simplifies the search of
k
nearest neighbors to that of a single
nearest neighbor, and no longer needs to compute the similarity between neighbor-
hoods.
It has been shown that the test complexities of KNN Offline-1 and KNN Offline-
2 are both
O(n
log
n)
, which is comparable with the single model approach. At the
same time, experimental results in [
5
] show that the effectiveness of these two offline
algorithms are comparable with KNN Online. Actually, it has been proven that the
approximations of KNN Online by KNN Offline-1 and KNN Offline-2 are accurate
in terms of difference in loss of prediction, as long as the learning algorithm used
is stable with respect to minor changes in training examples. And learning-to-rank
algorithms with regularization items in their loss functions, such as Ranking SVM,
are typical stable algorithms.
=