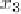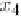Information Technology Reference
In-Depth Information
Fig. 6.1
The C-CRF model
6.1.2 Continuous Conditional Random Fields
In [
7
], Qin et al. also investigate the formalization of relational ranking, but using a
graphical model called continuous conditional random fields (C-CRF). C-CRF is a
graphical model, as depicted in Fig.
6.1
. In the conditioned undirected graph, a white
vertex represents a ranking score, a gray vertex represents a document, an edge
between two white vertexes represents the dependency between ranking scores, and
an edge between a gray vertex and a white vertex represents the dependency of a
ranking score on its document (content). (In principle a ranking score can depend on
all the documents of the query; here for ease of presentation we consider the simple
case in which it only depends on the corresponding document.)
Specifically, let
K
1
k
=
1
be a set of real-valued feature functions defined
on document set
x
and label
y
j
(
j
=
{
g
k
(y
j
,
x
)
}
K
2
k
{
g
k
(y
u
,y
v
,
x
)
}
1
,...,m
), and
be a set of
=
1
real-valued feature functions defined on
y
u
,
y
v
, and
x
(
u, v
v
). Then
C-CRF is a conditional probability distribution with the following density function,
=
1
,...,m
,
u
=
Z(
x
)
exp
j
β
k
g
k
(y
u
,y
v
,
x
)
,
K
1
K
2
1
Pr
(
y
|
x
)
=
α
k
g
k
(y
j
,
x
)
+
(6.7)
k
=
1
u,v
k
=
1
where
α
is a
K
1
-dimensional parameter vector and
β
is a
K
2
-dimensional parameter
vector, and
Z(
x
)
is a normalization function,
exp
j
β
k
g
k
(y
u
,y
v
,
x
)
d
y
.
K
1
K
2
Z(
x
)
=
α
k
g
k
(y
j
,
x
)
+
(6.8)
y
u,v
k
=
1
k
=
1
x
(i)
,
y
(i)
n
i
Given training data
{
}
1
, the Maximum Likelihood Estimation can be
=
used to estimate the parameters
of C-CRF. Specifically, the conditional log
likelihood of the training data with respect to the C-CRF model can be computed as
follows:
{
α, β
}
n
log Pr
y
(i)
;
α, β
.
x
(i)
L(α, β)
=
|
(6.9)
i
=
1