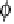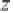Information Technology Reference
In-Depth Information
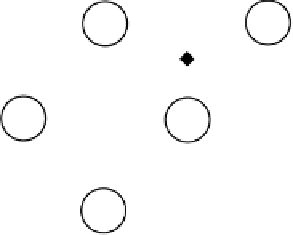
Fig. 4.2
The CDN model
An
example
is
shown
in
Fig.
4.2
.
In
the
example,
the
joint
CDF
F(z
1
,z
2
,z
3
,z
4
,z
5
)
φ
a
(z
2
)φ
b
(z
1
,z
2
,z
3
)φ
c
(z
3
)φ
e
(z
3
,z
4
,z
5
)φ
f
(z
5
)
.
When applied to learning to rank, the vertices in the CDN represent the docu-
ments to be ranked and the edges represent their preference relationships. Given
each edge in the CDN, the likelihood of the preference represented by the edge can
be defined by the
F(
=
·
)
function, which takes the following form in [
16
]:
1
F(z)
=
f(x
v
)))
,
(4.27)
+
−
−
+
−
θ
2
(f (x
u
)
−
1
exp
(
θ
1
(f (x
u
)
f(x
v
)))
exp
(
e,e
where
e
is the edge between nodes
x
u
and
x
v
and
e
is the edge between nodes
x
u
and
x
v
.
Then, the negative log likelihood of all the preferences captured by the graph is
used as the loss function for ranking. The algorithm that learns the ranking model
by minimizing this loss function is called StructRank.
As discussed in [
16
], ListNet [
4
] and ListMLE [
31
] can be regarded as special
cases of StructRank. Specifically, in these algorithms, the CDN function is defined
with
m
−
1 multivariate sigmoids: the first sigmoid is concerned with
m
−
1 edges,
the second with
m
−
2 edges,
...
, the last with only one edge. Furthermore, in certain
conditions, RankNet [
3
] can also be regarded as a special case of StructRank.
4.3.4 BoltzRank
In [
30
], a flexible ranking model is proposed, referred to as BoltzRank. BoltzRank
utilizes a scoring function composed of individual and pairwise potentials to define
a conditional probability distribution, in the form of a Boltzmann distribution, over
all permutations of documents retrieved for a given query.
Specifically, given a set of documents
x
m
={
x
j
}
j
=
1
, their ranking scores
s
=
m
j
{
1
, and the corresponding ranking
π
, the conditional energy of
π
given
s
is defined as follows:
f(x
j
)
}
=
1
)
u<v
2
m(m
−
E
[
π
|
s
]=
g
q
(v
−
u)
·
(s
π
−
1
(u)
−
s
π
−
1
(v)
),
(4.28)