Information Technology Reference
In-Depth Information
FIGURE 1.15
Element of a beam in bending and extension.
the curvature of the deflection curve is
d
θ/
dx
κ
=
/
(
1
+
θ
2
)
3
2
or for
θ
small relative to unity
d
θ
dx
κ
=
(1.97)
where
is the slope of the deflection curve.
We assume that regardless of the type of applied loading, the beam deforms as though
it were undergoing pure bending (a constant moment along the beam). This contention,
which is referred to as Bernoulli's
23
hypothesis, implies that cross-sections of the beam
remain planar and perpendicular to the longitudinal axis under bending. That is, for a
beam with arbitrary supports, changes in cross-section, or applied loading, it is assumed
that a “flat” cross-section remains “flat” as it deforms, which is how the beam would deform
if it were uniform and were subjected only to a constant moment along the beam. See an
elementary strength of materials text for an in-depth discussion of this beam theory. It
can be seen (Fig. 1.15) that for this deformation the axial displacement of a point on a
cross-sectional plane is
θ
u
(
x, z
)
=
u
0
(
x
)
+
z
θ(
x
)
(1.98)
where
u
0
is the axial displacement of the point at which the
x
axis intersects the cross-
sectional plane and
θ
=
tan
α
is the slope of the beam axis. For small
α
, it follows that
θ
≈
α
.
23
Daniel Bernoulli (1700-1782) was the son of Johann Bernoulli. He studied medicine and philosophy. Mathematics
instruction came from his father and his uncle Jakob. He is best known for his topic
Hydrodynamica,
and for his
efforts in the mechanics of flexible bodies. He suggested by letter to Euler that the calculus of variations be used
to derive the equations governing the elastic curve. As a consequence, the governing equations for engineering
beam theory are often referred to as Euler-Bernoulli equations.



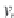

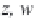














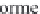
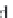




























Search WWH ::

Custom Search