Information Technology Reference
In-Depth Information
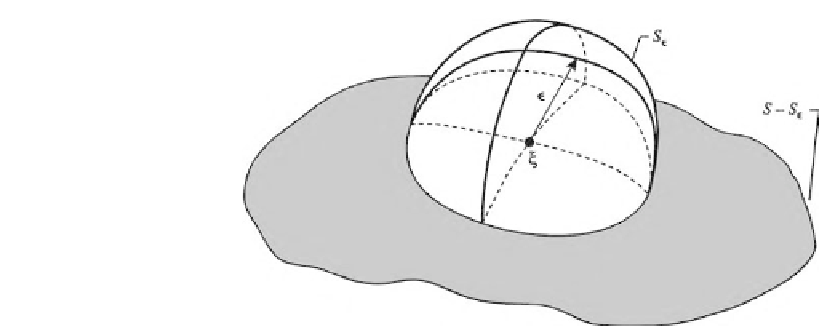
FIGURE 9.1
The boundary when
ξ
is moved to the boundary.
for two-dimensional problems, in which
r
i
is the component of
r
in the
x
i
direction. Equation (9.23) has the property that the unknown variable
u
inside of or on the
boundary of the domain is expressed in terms of
u
and its derivative
q
=
(
x
i
−
ξ
)
i
n
on the
boundary as well as in terms of the volume integral involving the known quantity
b
.If
=
∂
u
/∂
ξ
is moved to the boundary, Eq. (9.23) will be a relationship involving unknown variables
on the boundary only. When the point
is on the boundary, however, singularities in
u
∗
and
q
∗
develop and they must be given special consideration. These singularities occur
because when
ξ
; consequently,
the integrands of the boundary integrals of Eq. (9.23) involving
u
∗
and
q
∗
become singular.
To investigate how to overcome the singularity, assume that the boundary can be repre-
sented as shown in Fig. 9.1 where
ξ
is on the boundary,
r
of Eqs. (9.22) becomes zero at
x
=
ξ
S
=
(
S
−
S
)
+
S
in which
S
is a hemispherical surface of radius
. The second integral on the right-hand
side of Eq. (9.23) can be written as
qu
∗
dS
qu
∗
dS
qu
∗
dS
=
lim
→
+
lim
→
(9.24)
0
0
S
S
−
S
S
Consider the first integral on the right-hand side of (Eq. 9.24). Since no singularity occurs
on the part of the boundary
S
−
S
, the integral has no change when
→
0
,
i.e.,
qu
∗
dS
qu
∗
dS
lim
→
=
0
S
−
S
S
u
∗
=
For the second integral of (Eq. 9.24), substitution of the expression for
δ
u
=
1
/
r
of Eq. (9.22a) for three-dimensional problems into this integral leads to
0
q
1
qu
∗
dS
lim
→
=
lim
→
dS
0
S
S
2
sin
From Fig. 9.2,
dS
=
ϕ
d
ϕ
d
θ.
Then
0
q
2
2
π
0
π/
2
1
0
q
1
=
θ
ϕ
ϕ
=
π
=
lim
→
dS
lim
→
d
sin
d
lim
→
q
2
0
(9.25)
0
S
0







Search WWH ::

Custom Search