Information Technology Reference
In-Depth Information
x
a
X
FIGURE 5.10
Right-handed global
y,Y
(
X, Y, Z
)
and local
(
x, y, z
)
coordi-
z
nate systems. The angle
α
is positive as shown (vector
Z
corresponding to
α
is positive along positive
Y
axis).
Global to Local Forces and Displacements:
i
T
aa
0
0
bb
i
p
a
p
b
i
p
a
v
i
T
i
v
i
=
and
=
(5.22)
p
b
p
i
T
i
p
i
=
with, in more general notation, the transformation matrix
T
i
T
aa
i
T
ab
T
i
=
(5.23)
T
ba
T
bb
cos
α
−
sin
α
T
ba
=
T
ab
=
0
and
T
aa
=
T
bb
=
(5.24)
sin
α
cos
α
where
is the angle between the
X
(global coordinate) and the
x
(local) coordinate.
Observe that for
T
i
jj
,j
α
=
a
or
b
,defined by Eq. (5.24)
T
i
jj
T
i
jj
=
T
iT
T
i
=
I
,
I
(5.25)
where superscript
T
designates the transpose and
I
is the unit diagonal matrix. The coor-
dinate transformation for orthogonal coordinate axes always possesses this property. Since
(
T
i
)
−
1
T
i
=
I
, it follows that
T
i
)
−
1
T
iT
(
=
(5.26)
Hence, the transformation from local to global coordinates can be expressed as
Local to Global Forces and Displacements:
p
a
p
b
i
T
aa
0
0
bb
i
i
p
a
v
i
T
iT
v
i
=
and
=
(5.27)
p
b
p
i
T
iT
p
i
=
Stiffness matrices are readily transformed from one coordinate system to another. This is
accomplished by noting that
k
i
k
i
T
i
v
i
p
i
T
iT
p
i
T
iT
v
i
T
iT
=
=
=
Since
p
i
=
k
i
v
i
,
it follows that
k
i
T
i
(5.28)
A triple matrix product of this form is called a
congruent transformation
. The product
k
i
will be a symmetric matrix if the
k
i
k
i
T
iT
=
is symmetric. As indicated in the previous two chapters,
stiffness matrices are symmetric.








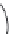











Search WWH ::

Custom Search