Environmental Engineering Reference
In-Depth Information
4
β
0
3
β
0
2
β
0
0
β
k
2
β
4
β
6
β
8
β
10
β
Figure 3.4. Scenario of the steady-state pdf's for the Verhulst model driven by sym-
metric multiplicative noise.
k
is the switching rate,
is the amplitude of the noise.
directly the expression of
p
(
φ
)givenby(
3.20
) we obtain
2
;
p
(0)
=∞
,
if
β
(2
k
+
β
)
<
φ
=
0
→∞
,
d
p
(
φ
)
2
p
(0)
=
0
,
if
β
(
k
+
β
)
<
<β
(2
k
+
β
);
d
φ
φ
=
0
=
d
p
(
φ
)
2
p
(0)
=
0
,
0
,
if
<β
(
k
+
β
)
.
d
φ
) are shown in Fig.
3.4
. We observe a remarkable variety
of possible behaviors (
Kitahara et al.
,
1980
), depending on the autocorrelation scale
τ
c
=
The different shapes of
p
(
φ
2
of noise. With respect to the additive case (see Fig.
3.2
),
we can recognize the impact of the multiplicative form of the noise, which induces
a greater variety of dynamical behaviors. In particular, in the case of multiplicative
noise the deterministic steady state
1
/
(2
k
) and amplitude
φ
=
β
is never a mode or antimode of the pdf
because
0, i.e., in the absence of noise.
In the case of asymmetric dichotomous noise (i.e.,
φ
=
β
is a solution of Eqs. (
3.22
) only if
=
1
=
2
) the third term in
Eq. (
3.3
) also plays a role, further increasing the variety of possible noise-induced
transitions.
3.2.1.3 Periodic forcing as a term of comparison
To understand the real role of noise in systems forced by a random dichotomous
driver, it is useful to assess whether qualitatively similar phenomena would appear if





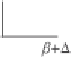

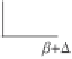

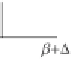






























Search WWH ::

Custom Search