Environmental Engineering Reference
In-Depth Information
0.75
IV
p A
p A
A
1
A
V
0
0.5
p A
p A
a
1
A
1
A
0
0
III
b
0.25
I
p A
c
II
1
A
0
0
0
1
2
3
a
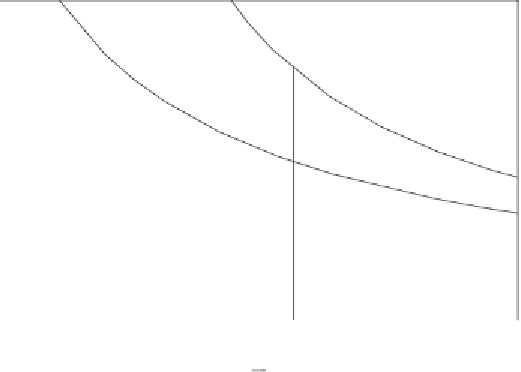
Figure 4.11. Dependence of the shape of the probability distribution
p
(
A
) of woody
biomass
A
on parameters of the fire-vegetation dynamics in the presence of positive
feedback between fire frequency and grass biomass (
b
=
0 with
b
<
0). Calculated
with the same parameters as in Fig.
4.9
but with
b
/
a
=−
0
.
7. With respect to the case
b
=
0 (i.e., Fig.
4.9
) line (c) shifts to the right, enabling a wider bistable domain, IV.
fire-vegetation feedback destabilizes conditions favorable to tree-grass coexistence
(i.e., the existence of a mode of
A
between 0 and 1), whereas grassland and woodland
become alternative stable states of the system, as shown in Fig.
4.12
. Notice that the
state dependence
λ
(
A
) only enhances this bistable behavior, and its emergence is
induced by the multiplicative noise (see previous section).
3
4.3.3 Stochastic soil-mass balance
In this section we provide an example of systems forced by multiplicative Poisson
noise, with a bound imposed on the distribution
p
(
h
) of the “jumps”
h
of the shot
noise [see Eq. (
4.9
)]. It is shown that the state dependency induced by this bound is
capable of leading to noise-induced transitions. This example is based on the dynamics
of soil production and erosion in landslide-prone landscapes. These dynamics were
traditionally investigated (
Kirkby
,
1971
;
Ahnert
,
1988
;
Dietrich et al.
,
1995
;
Roering
et al.
,
1999
) through a soil-mass-balance equation in which the variability in time of
3
In fact, the deterministic counterpart of the process with state-dependent rate of fire occurrence has only one unstable
state (
A
∗
=
0) and one stable state [
A
∗
=
(1
−
λα/
a
)
/
(1
+
α
b
/
a
)] that can be calculated with (
4.13
), replacing
λ
with
λ
=
λ
+
bA
.
























Search WWH ::

Custom Search