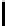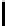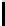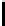Information Technology Reference
In-Depth Information
Solving MCKP is NP-hard, which is shown by reduction to a basic knapsack prob-
lem [10] (p. 318). Using dynamic programming, however, the problem can be solved
in pseudopolynomial time [11]. Let
Z
l
(
d
) be the value of the optimal solution to the
MCKP defined to include only the first
l
agents, 1
≤
≤
l
N
, and with restricted capacity
≤
≤
≤
≤
−
∞
for
d
<
0.
0
d
c
. We further define
Z
0
(
d
)=0for0
d
c
,and
Z
l
(
d
)=
≤
≤
≤
≤
We can characterize
Z
l
(
d
),1
l
N
,0
d
c
, using the following recursion:
q
lj
)+
p
lj
.
Z
l
(
d
)= max
1
≤
j
≤
m
l
Z
l
−
1
(
d
−
(1)
The optimal solution is obtained when
l
=
N
and
d
=
c
.Given
N
bids of maximum
size
m
= max
i
m
i
, the running time to solve MCKP using dynamic programming is
O
(
mNc
) [10]. If agents choose to submit full demand curves (i.e., with up to
C
bundles
each), the running time becomes
O
(
NC
2
).
Many different methods exist to solve MCKP, including a number of branch-and-
bound techniques and hybrid algorithms (see Kellerer et al. [10] for an extensive re-
view). Our implementation is customized for the dynamic auction context, which may
call for repeated solution of the MCKP for small changes in the set of bids. We therefore
developed an incremental version of the clearing algorithm, designed to minimize the
average solution time over a sequence of auction operations. Space constraints preclude
a description of the algorithm here; see the full paper for details.
2.2
Clearing and Pricing
Clearing
the auction is the process of identifying the subset of bids that match and pro-
duce the highest possible surplus. The outcome of a clear operation is to determine the
deals resulting from this matching, and removing the matched bids from the order book.
Given our incremental algorithm, most of the work is performed when bids are inserted
into the order book. Once this is done, identifying the match takes constant time. Ex-
tracting the deals takes time linear in the number
N
of bids matched. Modifying the
order topic to include only unmatched bids requires
N
deletions or (
N
N
) insertions.
Matching bids with indivisibility constraints and three or more agents requires non-
uniform pricing [12]. It is easy to understand the impossibility of having uniform pricing
through an example. Consider the bids in Table 1. In such example, the auction would
match all four bids. However, it is impossible to make all buyers pay at most what they
offered while making all sellers receive at least what they requested with a single price.
−
Ta b l e 1 .
Matching these bids requires non-uniform prices
(13 @ 26) buy 13 units at $2 each
(2 @ 1) buy 2 units at $0.5 each
(-11 @ -11) sell 11 units at $1 each
(-4 @ -10)
sell 4 units at $2.5 each
There are many ways to determine non-uniform prices consistent with a given set of
bids and an allocation. For a fixed allocation of goods, monetary transfers do not affect