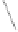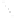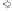Information Technology Reference
In-Depth Information
q=40
q=60
q=80
0.25
0.2
0.15
0.1
0.05
80
60
0
40
1
0.8
0.6
0.4
Weight
0.2
Shapley value
Fig. 8.
Shapley value and uncertainty for a game of 20 players and a varying weight
defined by
N
(4
X, X
) in the interval [
q
−
w
i
,q
−
], i.e.,
q−
1
(2
πν
)
(
x−
4
X
)
2
2
X
Δ
i
=
e
−
dx
(17)
q−w
i
and its Shapley value is
m
1
n
Δ
i
ϕ
i
=
(18)
X
=1
It is easy to verify that the time complexity of this method is
O
(
m
). Also, the two
sources of inaccuracy are
X
and
. As in the case of the randomised method of Sec-
tion 6, the inaccuracy decreases with
X
and increases with
. The uncertainty associated
with the Shapley value is:
m
1
n
Δ
i
)
2
β
i
=
(
ϕ
i
−
(19)
X
=1
For the case of more than two player types, we define the following constraints on
q
and
w
i
(for 1
≤
i
≤
m
):
C
3
No player can win the game on its own (i.e., (
w
i
<q
)for1
m
).
C
4
The number of players required to win an election is less than
m
(i.e., the quota is
less than 4
m
2
).
≤
i
≤
≤
m
), and
m
, such that constraints
C
3
and
C
4
are always satisfied, and determine the rela-
tion between the Shapley value and its uncertainty. These results are plotted in Figures
8 to 10. Consider Figure 8. For each quota, an individual player's weight is varied be-
tween 1 and
q
We use the above equations and systematically vary parameters
q
,
w
i
(for 1
≤
i
1. As seen in the figure, uncertainty first increases with Shapley value
and then decreases. Figure 9 is a plot for
m
=50and Figure 10 that for
m
= 100.In
all these figures, a player's uncertainty first increases with its Shapley value and then
decreases. Thus, the relation between the Shapley value and its uncertainty is the same
as that in Figure 1.
−