Information Technology Reference
In-Depth Information
x 10
−3
k=0.1
k=0.5
k=0.9
3
2.5
2
1.5
1
0.5
0
15
0.02
10
j
0.04
5
Shapley value
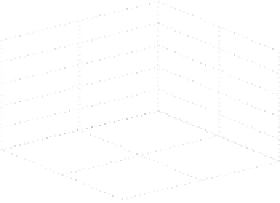
Fig. 2.
A large player's Shapley value and uncertainty for a varying weight
m
1
m
(
Δ
l
ϕ
l
)
2
β
l
=
−
(13)
X
=1
Consider a small party. The marginal contribution of this party, when added to a
sample, is one if the weight of the sample is less than the quota (
q
) but is greater than or
equal to (
q
−
1). Otherwise, its marginal contribution is zero. We know that the mean
weight of the sample is
kXj
+(1
k
)
X
.Let
c
denote the proportion of large players
that is required for the random sample to have mean weight (
q
−
−
1) (i.e.,
c
=(
q
−
−
1
X
)
/
(
X
(
j
1))). Also, let
d
denote the proportion of large players that is required for
the random sample to have mean weight
q
−
−
(i.e.,
d
=(
q
−
X
−
)
/
(
X
(
j
−
1))).
The marginal contribution of a small player is the area under the curve defined by the
normal distribution of Equation 10 between the limits
c
and
d
, i.e.,
d
1
(2
πν
)
(
x−μ
)
2
2
ν
Δ
s
=
e
−
dx
(14)
c
Therefore, for each small player, the Shapley value is:
m
1
m
Δ
s
ϕ
s
=
(15)
X
=1
and the uncertainty is:
m
1
m
(
Δ
s
ϕ
s
)
2
β
s
=
−
(16)
X
=1
Theorem 1.
The time complexity of the above randomised method for determining the
Shapley value is polynomial in the number of players. The inaccuracy of this method
decreases with
X
and increases with
.
Proof. The time required to compute the marginal contribution of a player to a coalition
of size
i
(for
1
m
) is independent of the number of players (see Equations 11 and
14). A player can join the coalition as the
i
th member (for
1
≤
i
≤
m
). The marginal
contribution of a player is determined for each of these
m
possible cases. Therefore,
the time taken to compute the Shapley value is
O
(
m
)
.
≤
i
≤