Shape as Memory Storage - Ambient Intelligence for Scientific Discovery - page 84

c 2 , while
always ensuring that it maintains the property of been tangential to the two
curves simultaneously. To maintain this double-touching property, it might be
necessary to expand or contract the circle. This procedure was invented by Blum
in the 1960s, and he defined the symmetry axis to be the center of the circle as it
moved. However, in my topic, Symmetry, Causality, Mind , I showed that there
are serious topological problems with this definition, and I defined the axis to
be the trajectory of the point Q shown in Fig 3. This is the point on the circle,
half-way between the two tangent points. As the circle moves along the curves, it
traces out a trajectory as indicated by the sequence of dots shown in the figure.
I called this axis, Process-Inferring Symmetry Axis , or simply PISA. It does not
have the problems associated with the Blum axis.

Next, move the circle continuously along the two curves, c 1 and

4 Symmetry-Curvature Duality

TheProcess-Grammartobeelaboratedrelies on two structural factors in a
shape: symmetry and curvature. Mathematically, symmetry and curvature are
two very different descriptors of shape. However, a theorem that I proposed and
proved in [4] shows that there is an intimate relationship between these two
descriptors. This relationship will be the basis of the entire chapter.

Symmetry-Curvature Duality Theorem (Leyton, 1987): Any section of
curve, that has one and only one curvature extremum, has one and only one
symmetry axis. This axis is forced to terminate at the extremum itself.

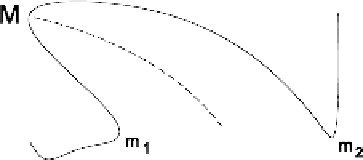
Fig. 4. Illustration of the Symmetry-Curvature Duality Theorem.

The theorem can be illustrated by looking at Fig 4. On the curve shown,
there are three extrema: m 1 , M ,and m 2 . Therefore, on the section of curve

between extrema . What the theorem

says is this: Because this section of curve has only one extremum, it has only
one symmetry axis. This axis is forced to terminate at the extremum

m 1 and m 2 , there is only one extremum, M

M .The

axis is shown as the dashed line in the figure.
It is valuable to illustrate the theorem on a closed shape, for example, that
shown in Fig 5. This shape has sixteen curvature extrema. Therefore, the above
theorem tells us that there are sixteen unique symmetry axes associated with,
and terminating at, the extrema. They are given as the dashed lines in the figure.