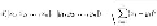Database Reference
In-Depth Information
that allows us to focus on nearby points without comparing all points. Other applications
3.5.1
Definition of a Distance Measure
Suppose we have a set of points, called a
space
. A
distance measure
on this space is a func-
tion
d
(
x, y
) that takes two points in the space as arguments and produces a real number, and
satisfies the following axioms:
(1)
d
(
x, y
) ≥ 0 (no negative distances).
(2)
d
(
x, y
) = 0 if and only if
x
=
y
(distances are positive, except for the distance from a
point to itself).
(3)
d
(
x, y
) =
d
(
y, x
) (distance is symmetric).
(4)
d
(
x, y
) ≤
d
(
x, z
) +
d
(
z, y
) (the
triangle inequality
).
The triangle inequality is the most complex condition. It says, intuitively, that to travel from
x
to
y
, we cannot obtain any benefit if we are forced to travel via some particular third point
z
. The triangle-inequality axiom is what makes all distance measures behave as if distance
describes the length of a shortest path from one point to another.
3.5.2
Euclidean Distances
The most familiar distance measure is the one we normally think of as “distance.” An
n-di-
mensional Euclidean space
is one where points are vectors of
n
real numbers. The conven-
tional distance measure in this space, which we shall refer to as the
L
2
-norm
, is defined:
That is, we square the distance in each dimension, sum the squares, and take the positive
square root.
It is easy to verify the first three requirements for a distance measure are satisfied. The
Euclidean distance between two points cannot be negative, because the positive square root
is intended. Since all squares of real numbers are nonnegative, any
i
such that
x
i
≠
y
i
forces
the distance to be strictly positive. On the other hand, if
x
i
=
y
i
for all
i
, then the distance is
clearly 0. Symmetry follows because (
x
i
−
y
i
)
2
= (
y
i
−
x
i
)
2
. The triangle inequality requires a
good deal of algebra to verify. However, it is well understood to be a property of Euclidean
space: the sum of the lengths of any two sides of a triangle is no less than the length of the
third side.