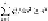Database Reference
In-Depth Information
Map function generates
g
key-value pairs. The key is the group of that element paired with
any of the groups of
M
, and the value is the element itself plus its row and column.
The Reduce Function
The reducer corresponding to the key (
i, j
), where
i
is a group of
M
and
j
is a group of
N
, gets a value list consisting of all the elements in the
i
th band of
M
and the
j
th band of
N
. It thus has all the values it needs to compute the elements of
P
whose
row is one of those rows comprising the
i
th band of
M
and whose column is one of those
comprising the
j
th band of
N
. For instance,
Fig. 2.11
suggests the third group of
M
and the
fourth group of
N
, combining to compute a square of
P
at the reducer (3
,
4).
Each reducer gets
n
(
n/g
) elements from each of the two matrices, so
q
= 2
n
2
/g
. The rep-
lication rate is
g
, since each element of each matrix is sent to
g
reducers. That is,
r
=
g
.
Combining
r
=
g
with
q
=
n
2
/g
we can conclude that
r
=
n
2
/q
. That is, just as for similarity
join, the replication rate varies inversely with the reducer size.
It turns out that this upper bound on replication rate is also a lower bound. That is, we
cannot do better than the family of algorithms we described above in a single round of
MapReduce. Interestingly, we shall see that we can get a lower total communication for the
same reducer size, if we use two passes of MapReduce as we discussed in
Section 2.3.9
.
We shall not give the complete proof of the lower bound, but will suggest the important
elements.
For step (1) we need to get an upper bound on how many outputs a reducer of size
q
can
cover. First, notice that if a reducer gets some of the elements in a row of
M
, but not all
of them, then the elements of that row are useless; the reducer cannot produce any output
in that row of
P
. Similarly, if a reducer receives some but not all of a column of
N
, these
inputs are also useless. Thus, we may assume that the best mapping schema will send to
each reducer some number of full rows of
M
and some number of full columns of
N
. This
reducer is then capable of producing output element
p
ik
if and only if it has received the
entire
i
th row of
M
and the entire
k
th column of
N
. The remainder of the argument for step
(1) is to prove that the largest number of outputs are covered when the reducer receives the
same number of rows as columns. We leave this part as an exercise.
However, assuming a reducer receives
k
rows of
M
and
k
columns of
N
, then
q
= 2
nk
,
and
k
2
outputs are covered. That is,
g
(
q
), the maximum number of outputs covered by a
reducer that receives
q
inputs, is
q
2
/
4
n
2
.
For step (2), we know the number of outputs is
n
2
. In step (3) we observe that if there are
k
reducers, with the
i
th reducer receiving
q
i
≤
q
inputs, then
or