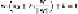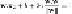Large-Scale Machine Learning - Mining of Massive Datasets - page 437

Figure 12.15 Normalizing the weight vector for an SVM
Our goal becomes to maximize γ , which is now the multiple of the unit vector w /|| w ||
between the separating hyperplane and the parallel hyperplanes through the support vec-
tors. Consider one of the support vectors, say x 2 shown in Fig. 12.15 . Let x 1 be the projec-
tion of x 2 onto the far hyperplane, also as suggested by Fig. 12.15 . Note that x 1 need not be
a support vector or even a point of the training set. The distance from x 2 to x 1 in units of
w /|| w || is 2 γ . That is,
(12.1)
Since x 1 is on the hyperplane defined by w . x + b = +1, we know that w . x 1 + b = 1. If we
substitute for x 1 using Equation 12.1 , we get
Regrouping terms, we see
(12.2)
But the first two terms of Equation 12.2 , w . x 2 + b , sum to −1, since we know that x 2 is on
the hyperplane w . x + b = −1. If we move this −1 from left to right in Equation 12.2 and
then divide through by 2, we conclude that
(12.3)
Notice also that w . w is the sum of the squares of the components of w . That is, w . w =
|| w || 2 . We conclude from Equation 12.3 that γ = 1/|| w ||.
This equivalence gives us a way to reformulate the optimization problem originally
stated in Section 12.3.1 . Instead of maximizing γ , we want to minimize || w ||, which is the
inverse of γ if we insist on normalizing the scale of w . That is,
• Given a training set ( x 1 , y 1 ), ( x 2 , y 2 ), . . . , ( x n , y n ), minimize || w || (by varying w and
b ) subject to the constraint that, for all i = 1, 2, . . . , n ,
y i ( w . x i + b ) ≥ 1