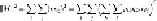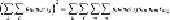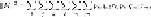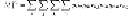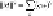Dimensionality Reduction - Mining of Massive Datasets - page 402

Then
(11.1)
When we square a sum of terms, as we do on the right side of Equation 11.1 , we effectively
create two copies of the sum (with different indices of summation) and multiply each term
of the first sum by each term of the second sum. That is,
we can thus rewrite Equation 11.1 as
(11.2)
Now, let us examine the case where P , Q , and R are really the SVD of M . That is, P is
a column-orthonormal matrix, Q is a diagonal matrix, and R is the transpose of a column-
orthonormal matrix. That is, R is row-orthonormal ; its rows are unit vectors and the dot
product of any two different rows is 0. To begin, since Q is a diagonal matrix, q kℓ and q nm
will be zero unless k = ℓ and n = m . We can thus drop the summations for ℓ and m in Equa-
tion 11.2 and set k = ℓ and n = m . That is, Equation 11.2 becomes
(11.3)
Next, reorder the summation, so i is the innermost sum. Equation 11.3 has only two
factors p ik and p in that involve i ; all other factors are constants as far as summation over i is
concerned. Since P is column-orthonormal, We know that ∑ i p ik p in is 1 if k = n and 0 other-
wise. That is, in Equation 11.3 we can set k = n , drop the factors p ik and p in , and eliminate
the sums over i and n , yielding
(11.4)
Since R is row-orthonormal, ∑ j r kj r kj is 1. Thus, we can eliminate the terms r kj and the
sum over j , leaving a very simple formula for the Frobenius norm:
(11.5)