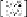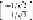Dimensionality Reduction - Mining of Massive Datasets - page 393

30 x + 28 y = 58 x
28 x + 30 y = 58 y
Both equations tell us the same thing: x = y . Thus, the unit eigenvector corresponding to
the principal eigenvalue 58 is
For the second eigenvalue, 2, we perform the same process. Multiply out
to get the two equations
30 x + 28 y = 2 x
28 x + 30 y = 2 y
Both equations tell us the same thing: x = − y . Thus, the unit eigenvector corresponding to
the principal eigenvalue 2 is
While we promised to write eigenvectors with their first component positive, we choose
the opposite here because it makes the transformation of coordinates easier to follow in this
case.
Now, let us construct E , the matrix of eigenvectors for the matrix M T M . Placing the prin-
cipal eigenvector first, the matrix of eigenvectors is
Any matrix of orthonormal vectors (unit vectors that are orthogonal to one another) rep-
resents a rotation of the axes of a Euclidean space. The matrix above can be viewed as a
rotation 45 degrees counterclockwise. For example, let us multiply the matrix M that rep-
resents each of the points of Fig. 11.1 by E . The product is
We see the first point, [ 1 , 2 ], has been transformed into the point
If we examine Fig. 11.2 , with the dashed line representing the new x -axis, we see that the
projection of the first point onto that axis places it at distance from the origin. To check