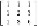Database Reference
In-Depth Information
EXERCISE
11.1.4 Find the eigenpairs for the following matrix:
using the method of
Section 11.1.2
.
!
EXERCISE
11.1.5 Find the eigenpairs for the following matrix:
using the method of
Section 11.1.2
.
EXERCISE
11.1.6 For the matrix of
Exercise 11.1.4
:
(a) Starting with a vector of three 1's, use power iteration to find an approximate value of
the principal eigenvector.
(b) Compute an estimate the principal eigenvalue for the matrix.
(c) Construct a new matrix by subtracting out the effect of the principal eigenpair, as in
(d) From your matrix of (c), find the second eigenpair for the original matrix of
Exercise
(e) Repeat (c) and (d) to find the third eigenpair for the original matrix.
EXERCISE
11.1.7 Repeat
Exercise 11.1.6
for the matrix of
Exercise 11.1.5
.
11.2 Principal-Component Analysis
Principal-component analysis
, or PCA, is a technique for taking a dataset consisting of
a set of tuples representing points in a high-dimensional space and finding the directions
along which the tuples line up best. The idea is to treat the set of tuples as a matrix
M
and
find the eigenvectors for
MM
T
or
M
T
M
. The matrix of these eigenvectors can be thought
of as a rigid rotation in a high-dimensional space. When you apply this transformation to
the original data, the axis corresponding to the principal eigenvector is the one along which
the points are most “spread out,” More precisely, this axis is the one along which the vari-
ance of the data is maximized. Put another way, the points can best be viewed as lying
along this axis, with small deviations from this axis. Likewise, the axis corresponding to
the second eigenvector (the eigenvector corresponding to the second-largest eigenvalue) is
the axis along which the variance of distances from the first axis is greatest, and so on.