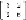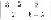Dimensionality Reduction - Mining of Massive Datasets - page 386

stochastic matrix, the limiting vector is the principal eigenvector (the eigenvector with the
largest eigenvalue), and its corresponding eigenvalue is 1. 2 This method for finding the
principal eigenvector, called power iteration , works quite generally, although if the prin-
cipal eigenvalue (eigenvalue associated with the principal eigenvector) is not 1, then as i
grows, the ratio of M i +1 v to M i v approaches the principal eigenvalue while M i v approaches
a vector (probably not a unit vector) with the same direction as the principal eigenvector.
We shall take up the generalization of the power-iteration method to find all eigenpairs
in Section 11.1.3 . However, there is an O ( n 3 )-running-time method for computing all the
eigenpairs of a symmetric n × n matrix exactly, and this method will be presented first.
There will always be n eigenpairs, although in some cases, some of the eigenvalues will be
identical. The method starts by restating the equation that defines eigenpairs, M e = λ e as
( M − λI ) e = 0 , where
(1) I is the n × n identity matrix with 1's along the main diagonal and 0's elsewhere.
(2) 0 is a vector of all 0's.
A fact of linear algebra is that in order for ( M − λI ) e = 0 to hold for a vector e ≠ 0 , the
determinant of M − λI must be 0. Notice that ( M − λI ) looks almost like the matrix M , but
if M has c in one of its diagonal elements, then ( M − λI ) has c −λ there. While the determ-
inant of an n × n matrix has n ! terms, it can be computed in various ways in O ( n 3 ) time; an
example is the method of “pivotal condensation.”
The determinant of ( M − λI ) is an n th-degree polynomial in λ, from which we can get the
n values of λ that are the eigenvalues of M . For any such value, say c , we can then solve
the equation M e = c e . There are n equations in n unknowns (the n components of e ), but
since there is no constant term in any equation, we can only solve for e to within a constant
factor. However, using any solution, we can normalize it so the sum of the squares of the
components is 1, thus obtaining the eigenvector that corresponds to eigenvalue c .
EXAMPLE 11.2 Let us find the eigenpairs for the 2 × 2 matrix M from Example 11.1 . Recall
M =
Then M − λI is
The determinant of this matrix is (3 − λ)(6 − λ) − 4, which we must set to 0. The equation
in λ to solve is thus λ 2 − 9λ + 14 = 0. The roots of this equation are λ = 7 and λ = 2; the first
is the principal eigenvalue, since it is the larger. Let e be the vector of unknowns