Database Reference
In-Depth Information
The
neighborhood profile
of a node
v
is the sequence of sizes of its neighborhoods |
N
(
v,
1)|
,
|
N
(
v,
2)|, . . . . We do not include the neighborhood of distance 0, since its size is always
1.
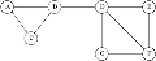
Fig. 10.23
.
To turn it into a directed graph, think of each edge as a pair of arcs, one in each
direction. For instance, the edge (
A, B
) becomes the arcs
A
→
B
and
B
→
A
. First, consider
the neighborhoods of node
A
. We know
N
(
A,
0) = {
A
}. Moreover,
N
(
A,
1) = {
A, B, C
},
since there are arcs from
A
only to
B
and
C
. Furthermore,
N
(
A,
2) = {
A, B, C, D
} and
N
(
A,
3) = {
A, B, C, D, E, F, G
}. Neighborhoods for larger radius are all the same as
N
(
A,
3).
Figure 10.23
Our small social network; think of it as a directed graph
On the other hand, consider node
B
. We find
N
(
B,
0) = {
B
},
N
(
B,
1) = {
A, B, C, D
}, and
N
(
B,
2) = {
A, B, C, D, E, F, G
}. We know that
B
is more central to the network than
A
, and
this fact is reflected by the neighborhood profiles of the two nodes. Node
A
has profile 3
,
4
,
7
,
7
, . . .
, while
B
has profile 4
,
7
,
7, . . . . Evidently,
B
is more central than
A
, because
at every distance, its neighborhood is at least as large as that of
A
. In fact,
D
is even more
central than
B
, because its neighborhood profile 5
,
7
,
7
, . . .
dominates the profile of each
of the nodes.
□
10.8.2
The Diameter of a Graph
The
diameter
of a directed graph is the smallest integer
d
such that for every two nodes
u
and
v
there is a path of length
d
or less from
u
to
v
. In a directed graph, this definition only
makes sense if the graph is
strongly connected
; that is, there is a path from any node to any
other node. Recall our discussion of the Web in
Section 5.1.3
,
where we observed that there
is a large strongly connected subset of the Web in the “center,” but that the Web as a whole
is not strongly connected. Rather, there are some pages that reach nowhere by links, and
some pages that cannot be reached by links.
If the graph is undirected, the definition of diameter is the same as for directed graphs,
but the path may traverse the undirected edges in either direction. That is, we treat an un-
directed edge as a pair of arcs, one in each direction. The notion of diameter makes sense
in an undirected graph as long as that graph is connected.