Database Reference
In-Depth Information
from the root to
Y
i
; this number was computed in Step 2 and is illustrated by the labels
After performing the credit calculation with each node as the root, we sum the credits
for each edge. Then, since each shortest path will have been discovered twice - once when
each of its endpoints is the root - we must divide the credit for each edge by 2.
We shall start from level 3 and proceed upwards. First,
A
and
C
, being leaves, get credit 1.
Each of these nodes have only one parent, so their credit is given to the edges (
B, A
) and
(
B, C
), respectively.
At level 2,
G
is a leaf, so it gets credit 1.
B
is not a leaf, so it gets credit equal to 1 plus
the credits on the DAG edges entering it from below. Since both these edges have credit 1,
the credit of
B
is 3. Intuitively 3 represents the fact that all shortest paths from
E
to
A
,
B
,
and
C
go through
B
.
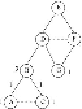
Figure 10.5
shows the credits assigned so far.
Figure 10.5
Final step of the Girvan-Newman Algorithm - levels 3 and 2
Now, let us proceed to level 1.
B
has only one parent,
D
, so the edge (
D, B
) gets the
entire credit of
B
, which is 3. However,
G
has two parents,
D
and
F
. We therefore need to
divide the credit of 1 that
G
has between the edges (
D, G
) and (
F, G
). In what proportion
do we divide? If you examine the labels of
Fig. 10.4
, you see that both
D
and
F
have label
1, representing the fact that there is one shortest path from
E
to each of these nodes. Thus,
we give half the credit of
G
to each of these edges; i.e., their credit is each 1/(1 + 1) = 0.5.
Had the labels of
D
and
F
in
Fig. 10.4
been 5 and 3, meaning there were five shortest paths
to
D
and only three to
F
, then the credit of edge (
D, G
) would have been 5/8 and the credit
of edge (
F, G
) would have been 3/8.
Now, we can assign credits to the nodes at level 1.
D
gets 1 plus the credits of the edges
entering it from below, which are 3 and 0.5. That is, the credit of
D
is 4.5. The credit of
F
is 1 plus the credit of the edge (
F, G
), or 1.5. Finally, the edges (
E, D
) and (
E, F
) receive
the credit of
D
and
F
, respectively, since each of these nodes has only one parent. These