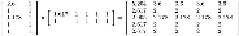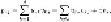Database Reference
In-Depth Information
−2 × (1.617(1 − 1.617
z
) + (2 −
z
) + (−
z
) + (3 −
z
)) = 0
whose solution is
z
= 6.617
/
5.615 = 1.178. The next estimate of the decomposition
UV
is
shown in
Fig. 9.16
.
□
Figure 9.16
Replace
z
by 1.178
9.4.4
Optimizing an Arbitrary Element
Having seen some examples of picking the optimum value for a single element in the mat-
rix
U
or
V
, let us now develop the general formula. As before, assume that
M
is an
n
-by-
m
utility matrix with some entries blank, while
U
and
V
are matrices of dimensions
n
-by-
d
and
d
-by-
m
, for some
d
. We shall use
m
ij
,
u
ij
, and
v
ij
for the entries in row
i
and column
j
of
M
,
U
, and
V
, respectively. Also, let
P
=
UV
, and use
p
ij
for the element in row
i
and column
j
of the product matrix
P
.
Suppose we want to vary
u
rs
and find the value of this element that minimizes the RMSE
between
M
and
UV
. Note that
u
rs
affects only the elements in row
r
of the product
P
=
UV
.
Thus, we need only concern ourselves with the elements
for all values of
j
such that
m
rj
is nonblank. In the expression above, we have replaced
u
rs
,
the element we wish to vary, by a variable
x
, and we use the convention
• ∑
k
≠
s
is shorthand for the sum for
k
= 1
,
2
, . . . , d
, except for
k
=
s
.
If
m
rj
is a nonblank entry of the matrix
M
, then the contribution of this element to the
sum of the squares of the errors is
We shall use another convention:
• ∑
j
is shorthand for the sum over all
j
such that
m
rj
is nonblank.
Then we can write the sum of the squares of the errors that are affected by the value of
x
=
u
rs
as