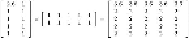Recommendation Systems - Mining of Massive Datasets - page 315

by changing a single entry. In what follows, we shall refer to entries of U and V by their
variable names u 11 , and so on, as given in Fig. 9.9 .
EXAMPLE 9.13 Suppose we start with U and V as in Fig. 9.10 , and we decide to alter u 11 to
reduce the RMSE as much as possible. Let the value of u 11 be x . Then the new U and V can
be expressed as in Fig. 9.11 .
Figure 9.11 Making u 11 a variable
Notice that the only entries of the product that have changed are those in the first row.
Thus, when we compare UV with M , the only change to the RMSE comes from the first
row. The contribution to the sum of squares from the first row is
(5 − ( x + 1)) 2 + (2 − ( x + 1)) 2 + (4 − ( x + 1)) 2 + (4 − ( x + 1)) 2 + (3 − ( x + 1)) 2
This sum simplifies to
(4 − x ) 2 + (1 − x ) 2 + (3 − x ) 2 + (3 − x ) 2 + (2 − x ) 2
We want the value of x that minimizes the sum, so we take the derivative and set that equal
to 0, as:
−2 × ((4 − x ) + (1 − x ) + (3 − x ) + (3 − x ) + (2 − x )) = 0
or −2 × (13 − 5 x ) = 0, from which it follows that x = 2.6.
Figure 9.12 shows U and V after u 11 has been set to 2.6. Note that the sum of the squares
of the errors in the first row has been reduced from 18 to 5.2, so the total RMSE (ignoring
average and square root) has been reduced from 75 to 62.2.
Figure 9.12 The best value for u 11 is found to be 2.6
Suppose our next entry to vary is v 11 . Let the value of this entry be y , as suggested in Fig.
9.13 . Only the first column of the product is affected by y , so we need only to compute the
sum of the squares of the differences between the entries in the first columns of M and UV .
This sum is