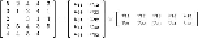Database Reference
In-Depth Information
9.4.1
UV-Decomposition
Consider movies as a case in point. Most users respond to a small number of features; they
like certain genres, they may have certain famous actors or actresses that they like, and per-
haps there are a few directors with a significant following. If we start with the utility matrix
M
, with
n
rows and
m
columns (i.e., there are
n
users and
m
items), then we might be able
to find a matrix
U
with
n
rows and
d
columns and a matrix
V
with
d
rows and
m
columns,
such that
UV
closely approximates
M
in those entries where
M
is nonblank. If so, then we
have established that there are
d
dimensions that allow us to characterize both users and
items closely. We can then use the entry in the product
UV
to estimate the corresponding
blank entry in utility matrix
M
. This process is called
UV-decomposition
of
M
.
EXAMPLE
9.11 We shall use as a running example a 5-by-5 matrix
M
with all but two of
its entries known. We wish to decompose
M
into a 5-by-2 and 2-by-5 matrix,
U
and
V
, re-
spectively. The matrices
M
,
U
, and
V
are shown in
Fig. 9.9
with the known entries of
M
indicated and the matrices
U
and
V
shown with their entries as variables to be determin-
ed. This example is essentially the smallest nontrivial case where there are more known
entries than there are entries in
U
and
V
combined, and we therefore can expect that the
best decomposition will not yield a product that agrees exactly in the nonblank entries of
M
.
□
Figure 9.9
UV-decomposition of matrix
M
9.4.2
Root-Mean-Square Error
While we can pick among several measures of how close the product
UV
is to
M
, the typical
choice is the root-mean-square error (RMSE), where we
(1) Sum, over all nonblank entries in
M
the square of the difference between that entry
and the corresponding entry in the product
UV
.
(2) Take the mean (average) of these squares by dividing by the number of terms in the
sum (i.e., the number of nonblank entries in
M
).
(3) Take the square root of the mean.
Minimizing the sum of the squares is the same as minimizing the square root of the average
square, so we generally omit the last two steps in our running example.