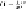Database Reference
In-Depth Information
system uses blocks of 64K bytes (i.e., 2
16
= 65,536 bytes to be exact). It takes approxim-
ately ten milliseconds to
access
(move the disk head to the track of the block and wait for
the block to rotate under the head) and read a disk block. That delay is at least five orders of
magnitude (a factor of 10
5
) slower than the time taken to read a word from main memory,
so if all we want to do is access a few bytes, there is an overwhelming benefit to having
data in main memory. In fact, if we want to do something simple to every byte of a disk
block, e.g., treat the block as a bucket of a hash table and search for a particular value of
the hash-key among all the records in that bucket, then the time taken to move the block
from disk to main memory will be far larger than the time taken to do the computation.
By organizing our data so that related data is on a single
cylinder
(the collection of blocks
reachable at a fixed radius from the center of the disk, and therefore accessible without
moving the disk head), we can read all the blocks on the cylinder into main memory in con-
siderably less than 10 milliseconds per block. You can assume that a disk cannot transfer
data to main memory at more than a hundred million bytes per second, no matter how that
data is organized. That is not a problem when your dataset is a megabyte. But a dataset of
a hun dred gigabytes or a terabyte presents problems just accessing it, let alone doing any-
thing useful with it.
1.3.5
The Base of Natural Logarithms
The constant
e
= 2
.
7182818 · · · has a number of useful special properties. In particular,
e
is the limit of as
x
goes to infinity. The values of this expression for
x
= 1
,
2
,
3
,
4 are
approximately 2
,
2
.
25
,
2
.
37
,
2
.
44, so you should find it easy to believe that the limit of this
series is around 2.72.
Some algebra lets us obtain approximations to many seemingly complex expressions.
Consider (1 +
a
)
b
, where
a
is small. We can rewrite the expression as (1 +
a
)
(1/
a
)(
ab
)
. Then
substitute
a
= 1/
x
and 1/
a
=
x
, so we have
which is
Since
a
is assumed small,
x
is large, so the subexpression
will be close to the limiting
value of
e
. We can thus approximate (1 +
a
)
b
as
e
ab
.
Similar identities hold when
a
is negative. That is, the limit as
x
goes to infinity of is
1/
e
. It follows that the approximation (1 +
a
)
b
=
e
ab
holds even when
a
is a small negative
number. Put another way, (1 −
a
)
b
is approximately
e
−ab
when
a
is small and
b
is large.
Some other useful approximations follow from the Taylor expansion of
e
x
. That is,
or
e
x
= 1 +
x
+
x
2
/2 +
x
3
/6 +
x
4
/24 + · · ·. When
x
is large, the above series converges slowly,