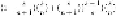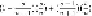Mining Data Streams - Mining of Massive Datasets - page 144

keep their same positions. However, if the ( n + 1)st position is picked, then throw out one
of the current s variables, with equal probability. Replace the one discarded by a new vari-
able whose element is the one at position n + 1 and whose value is 1.
Surely, the probability that position n + 1 is selected for a variable is what it should be:
s /( n + 1). However, the probability of every other position also is s /( n + 1), as we can prove
by induction on n . By the inductive hypothesis, before the arrival of the ( n + 1)st stream
element, this probability was s / n . With probability 1− s /( n +1) the ( n +1)st position will not
be selected, and the probability of each of the first n positions remains s / n . However, with
probability s /( n + 1), the ( n + 1)st position is picked, and the probability for each of the
first n positions is reduced by factor ( s − 1)/ s . Considering the two cases, the probability of
selecting each of the first n positions is
A General Stream-Sampling Problem
Notice that the technique described in Section 4.5.5 actually solves a more general problem. It gives us a way to main-
tain a sample of s stream elements so that at all times, all stream elements are equally likely to be selected for the
sample.
As an example of where this technique can be useful, recall that in Section 4.2 we arranged to select all the tuples
of a stream having key value in a randomly selected subset. Suppose that, as time goes on, there are too many tuples
associated with any one key. We can arrange to limit the number of tuples for any key K to a fixed constant s by using
the technique of Section 4.5.5 whenever a new tuple for key K arrives.
This expression simplifies to
and then to
which in turn simplifies to
Thus, we have shown by induction on the stream length n that all positions have equal
probability s / n of being chosen as the position of a variable.