Information Technology Reference
In-Depth Information
pentagons (60 vertices), is one of 13 Archimedes' solids (realized by two types of
regular polygons). Its shape corresponds to the standard football sphere. In 1985, a
molecule consisting of 60 atoms of carbon, called
Fullerene
, was discovered which
corresponds exactly to Archimedes' polyhedron of 60 vertices, 90 edges, and 32
faces, called
truncated icosahedron
, which is obtained by cutting all 12 vertices of
the icosahedron, and thus replacing them with pentagons as new faces (and con-
temporarily, doubling the edges of the other faces, which pass from triangles to
hexagons). Fullerene molecules and similar polyhedron molecules, with different
number of vertices, have very important chemical properties and the scientists who
discovered
C
60
(Robert F. Curl Jr., Sir Harold Kroto, Richard E. Smalley) won the
Nobel prize in 1996.
Colorability of graphs is another important subject of investigation. A graph is
k
-colorable if it is possible to assign one of
k
different colors to each of its node, in
such a way that nodes with a common edge have different colors (if a graph is
k
-
colorable, then it is also
k
1-colorable). An important result proves that any planar
graph is 4-colorable. Kenneth Appel and Wolfgang Haken proved this fact in 1976
by means of a computer program for analyzing a huge number of possibilities (1936
cases, and 633 cases in a more recent proof by other authors. Previous proofs, since
the end of 19th century, turned out to be wrong). The reader is advised to check that
the graph of Fig. 7.13 is 2-colorable, while the graph of Fig. 7.14 is not 4-colorable
(it is 5-colorable).
It was proved by Kuratowski in 1930 that a graph is planar if and only if it does
not “include” graph
K
3
,
3
of Fig. 7.13 or five-complete graph
K
5
of Figure 7.14. In
more formal terms, here the forbidden inclusion means that the given graph does
not include any expansion of
K
3
,
3
or
K
5
, where an expansion of a graph is realized
by replacing in it an edge between two nodes with a path between them. Fig. 7.18
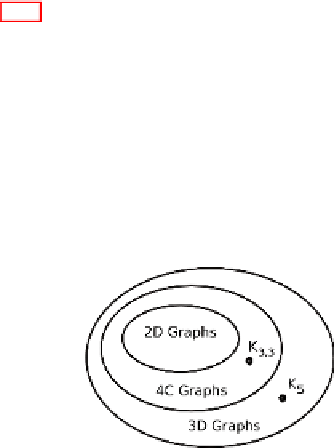
shows that non-planar graphs (3D, or three-dimensional) strictly include 4-colorable
graphs (4C), which strictly include planar graphs (2D, or 2-dimensional).
+
Fig. 7.18
Inclusions among graph planarity, 4-colorability, and non-planarity
We conclude the section by noting that the notion of duality of graphs is a case of
a general phenomenon of mathematics, which occurs in many forms and provides
very often an important key of comprehension of basic concepts. The simplest ex-
ample of duality is between elements and classes. A class contains elements, but an
element can be characterized by the classes to which it belongs. Analogously, a text