Information Technology Reference
In-Depth Information
7.8.3
Graph Planarity and Colorability
The theory of graphs started with Euler (1707-1793) who posed a problem inspired
from the river bridges in the city of Konisberg. The question was: “Is it possible
to cross all seven bridges of Konisberg in such a way that all of them are crossed
one and only one time?” In general terms, given a (non-oriented) graph we say that
a path along the nodes of the graph is
Eulerian
if every edge of the graph occurs
exactly once in the path. Euler found a sufficient and necessary condition that a
graph has to fulfill for the existence of such a path. Namely, if every node has even
degree, that is, an even number of edges connected to it, then when we enter into a
node we can exit from it by passing through another edge. But if some node has an
odd degree, this manner of visiting a node cannot be realized, and necessarily some
edge has to be crossed more than once.
Agraphis
planar
when it can be drawn in the plane in such a way that its
edges do not intersect. For example, it is easy to realize that the graph of Fig. 7.13,
consisting of two sets
A
and
B
having both three nodes and where each node of
A
is connected, by one edge, to every node of
B
is not a planar graph. Any tree is a
planar graph.
A
polyhedron
is a convex region of space bounded by polygons (for every pair
of points in the region, every point on the straight line segment that joins them is
also within the region). A polyhedron is “equivalent” to a planar graph. The follow-
ing construction provides the graph
G
naturally associated to a polyhedron
P
:
remove one face
f
from
P
(without removing its edges and vertices), then all ver-
tices and edges of
P
can be placed on the plane of
f
(the faces of
P
correspond to
minimal cycles (no subset of nodes of a minimal cycle is a cycle too). Now, consider
the portion of plane external to
G
(
P
)
(
)
(
)
P
as a face too, then
P
and
G
P
have the same
numbers of vertices, edges, and faces.
Euler proved that convex polyhedra satisfy a relation among the number
V
of its
vertices, the number
E
of its edges, and the number
F
of its faces. According to
the equivalence between polyhedra and planar graphs, this relation, also known as
Euler's
polyhedral formula
, can be proved for connected planar graphs.
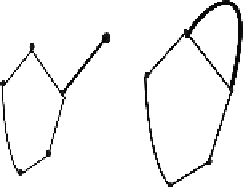
Fig. 7.16
Adding to a graph a new node and an edge (left) or only one edge (right)