Numbers and Measures - Infobiotics: Information in Biotic Systems - page 224

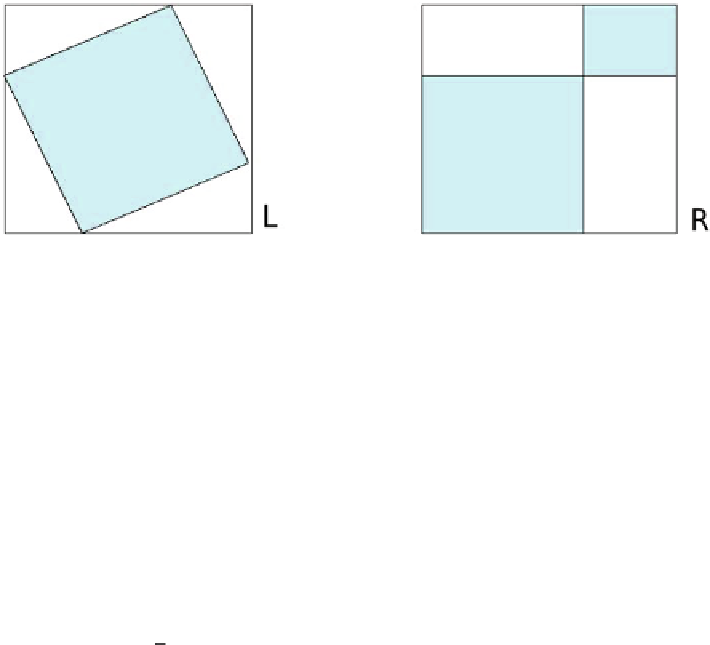
Fig. 5.4 Chinese proof of Pytagoras' theorem. The area of the left and right squares L, R is
the same. The internal square of L is obtained by removing four triangles from L. These four
triangles are equivalent to the two rectangles removed from the right rectangle R. Therefore,
the areas of the internal figures of L and R are equal

proof of the formula providing the sine of the angle . Angles are measured by

radiants , where a radiant is the angle corresponding to an arc with the same length
of the radius (so that 2

α + β

is the measure of a whole rotation, of 360 degrees). The
segment between double circles is sin

π

( α + β )

. It is the sum of two projections (bold
lines). In fact, the segment between the small and big full circles is cos β , and its

vertical projection (the smaller bold segment) is sin α cos β , while the segment be-

tween the double circle and the big full circle is sin β and its vertical projection (the

bigger bold segment) is sin β cos α . The sum of the two projections (bold lines) is

sin ( α + β ) .

The number √ 2 is irrational, but it is the root of the equation x 2 = 2, that is, it

is algebraic , while the number cannot be obtained as root of some equation with

rational coefficients. Irrational numbers which are not algebraic are called tran-
scendental . However, there are many formulae and algorithms for generating all

π

the digits of √ 2, as well as all the digits of

. Real numbers for which procedures
are known which generate the sequence of their digits are called computable real
numbers . When the notion of computable number was definitely clarified, after a
seminal paper of Turing (1936), it was completely clear that computable real num-
bers form a very small (in terms which can be mathematically formalized) subset of
all real numbers. In conclusion, we can define sets having elements which we can
collectively identify, albeit most of them have no individual identification process.
All the sets of numbers

π

are infinite. However, there is a crucial
difference between the sets of natural, integer, and rational numbers, from one side,
and the sets of real and complex numbers, on the other side. In fact, elements of
N , Z , Q

N , Z , Q , R , C

R
require, in general, infinite sequences of symbols. It can be shown that any infinite
set of finite sequences is enumerable , that is, it can be put in one-to-one correspon-
dence with the natural numbers. This kind of correspondence cannot be established
between the natural numbers and the set of all infinite sequences over a finite alpha-
bet. This means that real numbers are many more than the rationals. We can express

are represented by suitable finite sequences of symbols, while those of