Geology Reference
In-Depth Information
a thin layer of water, surface tensions will cause enor-
mous problems, and it will be impossible to simulate
tidal range and currents. Equally, material scaled down
to represent sand in the real system would be so tiny
that most of it would float. These problems of scaling
are usually surmountable, to a certain extent at least, and
scale models are used to mimic the behaviour of a variety
of geomorphic systems. For example, scale models have
assisted studies of the dynamics of rivers and river systems
using waterproof troughs and flumes.
Analogue models
are more abstract scale models. The
most commonly used analogue models are maps and
remotely sensed images. On a map, the surface features of
a landscape are reduced in scale and represented by sym-
bols: rivers by lines, relief by contours, and spot heights by
points, for instance. Remotely sensed images represent,
at a reduced scale, certain properties of the landscape
systems. Maps and remotely sensed images are, except
where a series of them be available for different times,
static analogue models. Dynamic analogue models may
also be built. They are hardware models in which the sys-
tem size is changed, and in which the materials used are
analogous to, but not the same as, the natural materials of
the system. The analogous materials simulate the dynam-
ics of the real system. In a laboratory, the clay kaolin can
be used in place of ice to model the behaviour of a val-
ley glacier. Under carefully controlled conditions, many
features of valley glaciers, including crevasses and step
faults, develop in the clay. Difficulties arise in this kind
of analogue model, not the least of which is the prob-
lem of finding a material that has mechanical properties
comparable to the material in the natural system.
Conceptual models
are initial attempts to clarify
loose thoughts about the structure and function of a
geomorphic system. They often form the basis for the
construction of mathematical models.
Mathematical
models
translate the ideas encapsulated in a conceptual
model into the formal, symbolic logic of mathematics.
The language of mathematics offers a powerful tool of
investigation limited only by the creativity of the human
mind. Of all modes of argument, mathematics is the most
rigorous. Nonetheless, the act of quantification, of trans-
lating ideas and observations into symbols and numbers,
is in itself nothing unless validated by explanation and
prediction. The art and science of using mathematics
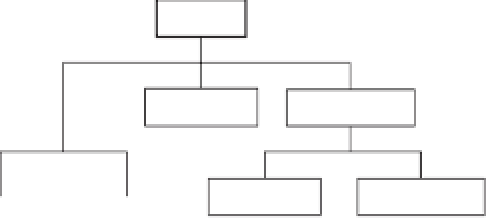
Models
Hardware
Conceptual
Mathematical
Scale
Analogue
Probabilistic
Deterministic
Increasing abstraction
Figure 1.12
Types of model in geomorphology.
Source:
After Huggett (1993, 4)
case, a
hardwaremodel
represents the system (see Mosley
and Zimpfer 1978). There are two chief kinds of hard-
ware model: scale models and analogue models.
Scale
(or
iconic
)
models
are miniature, or sometimes gigan-
tic, copies of systems. They differ from the systems they
represent only in size. Relief models, fashioned out of
a suitable material such as plaster of Paris, have been
used to represent topography as a three-dimensional sur-
face. Scale models need not be static: models made using
materials identical to those found in Nature, but with
the dimensions of the system scaled down, can be used
to simulate dynamic behaviour. In practice, scale models
of this kind imitate a portion of the real world so closely
that they are, in effect, 'controlled' natural systems. An
example is Stanley A. Schumm's (1956) use of the bad-
lands at Perth Amboy, New Jersey, to study the evolution
of slopes and drainage basins. The great advantage of this
type of scale model, in which the geometry and dynam-
ics of the model and system are virtually identical, is that
the investigator wields a high degree of control over the
simplified experimental conditions. Other scale models
use natural materials, but the geometry of the model is
dissimilar to the geometry of the system it imitates -
the investigator scales down the size of the system. The
process of reducing the size of a system creates a num-
ber of awkward problems associated with scaling. For
instance, a model of the Severn Estuary made at a scale
of 1 : 10,000 can easily preserve geometrical and topo-
graphical relationships. However, when adding water, an
actual depth of water of, say, 7 m is represented in the
model by a layer of water less than 0.7 mm deep. In such