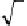Environmental Engineering Reference
In-Depth Information
z
(β
)
=
[9.33]
t
with which, [9.32] becomes:
β
d
θ
d
⎡
d
θ
⎤
−
=
D
[9.34]
⎢
⎣
⎥
⎦
θ
d
2
d
β
d
β
β
which is now an ordinary differential equation. Its solution gives β(θ) profiles that
are independent of
z
and
t
. This can be experimentally verified if water contents
measured during an infiltration test at different times and for different positions are
gathered on the same profile plotted
versus
β.
Inverting [9.33] gives:
z
=
(β
)
t
[9.35]
that straightforwardly explains the √
t
evolution observed for the wetting front
position
z
: the evolution is because infiltration is a diffusion phenomenon for which
[9.34] is valid. The total amount of water
I(t)
that has penetrated the sample at time
t
can be calculated by integrating the water content profile θ(
z
) inside the sample:
∆
m
(
t
)
z
θ
[
]
∫
max
∫
0
2
I
(
t
)
[kg/m
]
=
=
ρ
θ
(
z
)
−
θ
.
dz
=
ρ
z
(
θ
).
d
θ
[9.36]
l
i
l
s
0
θ
i
with:
s
: infiltrating surface [m
2
];
z
max
: sample height [m];
θ
i
: uniform initial sample water content; and
θ
0
: water content at the bottom of the sample (
z
= 0). Normally equal to porosity.
Substituting [9.35] into [3.36], we get:
ρ
θ
θ
=
∫
0
I
(
t
)
β
(
).
d
θ
t
=
ρ
S
t
=
A
t
[9.37]
l
l
c
i
This equation shows that
I(t)
must also be a function of √
t
, and gives a physical
significance to the
A
coefficient that, moreover, can be related to water diffusivity
D
θ
by [KUT 94]: