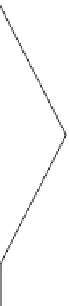Geoscience Reference
In-Depth Information
Theorem 7.11 (Brimberg et al.
2009b
)
Let
d
be the Euclidean distance, and
consider the planar case, i.e., let
D
D
2
. Then there exists a minsum circle which
passes through two points of
V
.
The result has been shown by looking at the second derivatives of the objective
function (in an appropriately defined neighborhood) which reveal that a circle
passing through exactly one or none of the existing points cannot be a local
minimum.
An algorithmic consequence of Theorem
7.11
is that there exists an optimal
circle with center point x being on a bisector of two of the existing points, hence
a line search along the bisectors is possible. Using Theorem
7.10
a large amount
of bisectors may be excluded beforehand. Figure
7.5
shows the Euclidean bisectors
for five existing facilities where the relevant parts (which contain center points of
circles having the halving property) are marked in bold.
Another approach was followed in Drezner and Brimberg (
2014
): Here the
unweighted case is shown to be an ordered median
point
location problem with
weights
D
.
1;:::;
1;1;:::;1/with equal number of
1's and 1's if n is even,
and with weights
D
.
1;:::;
1;0;1;:::;1/with equal number of
1's and 1's
if n is odd. The resulting ordered median point location problem was then solved
using the Big-Triangle-Small-Triangle method (Drezner and Suzuki
2004
) with the
d.c. bounding technique proposed in Brimberg and Nickel (
2009
).
B
12
B
14
B
24
B
15
B
25
v
3
B
34
v
1
v
2
B
35
v
4
B
45
v
5
B
23
B
13
Fig. 7.5
The Euclidean bisectors for five existing points. The notation B
ij
indicates that the
corresponding line is the bisector for points v
i
and v
j
. The parts of the bisectors which may contain
a center point of a minsum circle are marked in
bold