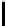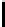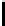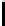Information Technology Reference
In-Depth Information
Table 3.
Thecaseof
{α
1
, ..., α
n
}
=
{x
n
−
1
,x
n
−
2
, ..., x,
1
}
n period max
τ
=0
|C
S
(
τ
)
|
of max
τ
=0
|C
S
(
τ
)
|
of
A
(
x
)=
Tr
(
x
2
n
−
2
)
A
(
x
)=
Tr
(
x
2
n
−
4
)
5
32
12
12
6
64
12
24
7
128
24
28
8
256
48
36
9
512
64
56
10 1024
104
108
11 2048
140
172
12 4096
204
304
13 8192
304
352
14 16384
488
456
15 32768
712
736
16 65536
1100
1472
17 131072
1548
1548
18 262144
2272
2656
The rest of the proof is the same as that of Theorem 2, so we omit it here.
Remark 2.
In [9], Niederreiter and Winterhof studied the distribution of
(
ξ
i
,ξ
i
τ
) implicitly for
τ>
0, where
i
j
=
h
if and only if
ξ
i
+
ξ
j
=
ξ
h
.
In general,
ξ
i
+
τ
=
ξ
i
τ
. Hence, we can not derive an upper bound on
C
S
(
τ
)
using the discrepancy bound in [9] together with the result in [6].
For many different bases, we computed max
τ
=0
|
F
2
18
in cases
of
A
(
x
)=
Tr
(
x
2
n
−
2
)and
A
(
x
)=
Tr
(
x
2
n
−
4
). We found that max
τ
=0
|
C
S
(
τ
)
|
from
F
2
5
to
C
S
(
τ
)
|
is
small compared with the period of sequences; namely,
2
n/
2
2
n/
2
2
.
12
×
≤
max
τ
=0
|
C
S
(
τ
)
|≤
5
.
75
×
18 and
A
(
x
)=
Tr
(
x
2
n
−
2
)or
Tr
(
x
2
n
−
4
). Based on these
in the case of 5
≤
n
≤
data, we present the following conjecture.
Conjecture 1.
For any sequence
S
defined by (1) with
p
=2and
A
(
x
)=
Tr
(
x
2
n
2
)or
A
(
x
)=
Tr
(
x
2
n
−
−
4
), there exists one constant
a
such that
2
n/
2
max
τ
=0
|
C
S
(
τ
)
|≤
a
·
holds for all
n
.
The experimental results are shown in Tables 2 and 3. Table 2 is for the case of
{
1
,x,x
2
, ..., x
n−
1
α
1
, ..., α
n
}
=
{
}
, and Table 3 is for the case of
{
α
1
, ..., α
n
}
=
x
n−
1
,x
n−
2
, ..., x,
1
{
}
.