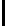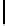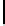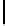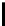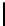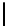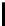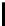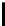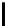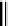Information Technology Reference
In-Depth Information
t
=0
2
n
t
2
i
=0
(
i
)
+
i
=0
(
i
)
<
2
n−s
.
(4)
2
n
If this upper bound is at most 1, then we deduce that
P
s,r,D
<
1 and this proves
that there exist permutations
F
from
F
2
to itself whose higher order nonlinearity
nl
s,r
(
F
) is strictly greater than
D
. This completes the proof.
We give in Table 5 below the values obtained from Lemma 1, such that, for each
of them, there surely exists a permutation
F
whose higher nonlinearity
nl
s,r
(
F
)
is not smaller. Note that since the weight of a Boolean function of algebraic
degree strictly smaller than
n
is even, we could increase any odd number in this
table by 1 (but we prefer leaving the values as they are given by Lemma 1). Note
also that these lower bounds may be improved by using the results by Kasami
et al. [37,38,39] on the values of
A
s,i
when
i
2
n−s
.
We are also interested in what happens when
n
tends to
≤
2
.
5
·
∞
.Let
H
2
(
x
)=
−
x
) be the entropy function.
Proposition 8.
Let
s
n
be a sequence of integers tending to
x
log
2
(
x
)
−
(1
−
x
)log
2
(1
−
∞
and such that,
asymptotically,
s
n
≤
.
227
n
. Then for every sequence
r
n
and
D
n
of positive
Table 5.
Lower bounds, deduced from Lemma 1, on the highest possible values of
nl
s,r
(
F
), when
F
is a permutation and for
n ≤
12
n s r
=1
2
3
4
5
6
7
8
9
4
1
2
5
1
6
3
2
2
6
1
16
9
4
2
6
2
7
1
39
26
13
4
2
16
10
3
8
1
89
66
39
17
5
2
42
31
15
2
3
7
2
9
1
196
158
105
54
21
5
2
99
83
52
19
3
25
17
3
10 1
422
359
261
156
73
25
6
2
219
196
145
77
20
3
72
60
33
11 1
890
788
614
408 223 95
30
7
2
466
436
356
229 100 13
3
178
163
119
48
4
15
8
12 1
1849 1686 1389 1004 615 308 121 35
7
2
969
931
814
597 332 112
3
409
388
324
197
44
4
82
71
36