Information Technology Reference
In-Depth Information
1-decimation
x
3
x
2
x
1
x
0
carry
out
c
0
a
b
1
r
1
2-decimation
c
0
a
b
0
r
0
x
3
x
1
carry
in
x
2
x
0
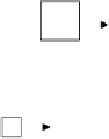
(a) Galois FCSR for
q
= 19.
(b) 2-bit ripple carry adder.
Fig. 6.
Example for a Galois FCSR with
q
=19
The case of Galois FCSRs is more dicult because the circuit can not be split
into two parts: each bit of the carry register must be handle separately. The
modification of the basic operator of a Galois FCSR,
i.e.
addition with carry, is
the key transformation to obtain a sub-sequences generator. Let us consider a
Galois FCSR with
q
= 19. This automaton has a single addition with carry as
shown in Figure 6(a). The sub-sequences generator for
d
= 2 associated to this
FCSR is defined by:
t
+1
(
x
0
)
t
+1
=(
x
0
)
t
⊕
(
x
1
)
t
⊕
(
c
0
)
t
(8)
(
c
0
)
t
+1
=[(
x
0
)
t
⊕
(
x
1
)
t
][(
x
0
)
t
⊕
(
c
0
)
t
]
⊕
(
x
0
)
t
t
+2
(
x
0
)
t
+2
=(
x
0
)
t
+1
⊕
(
x
2
)
t
⊕
(
c
0
)
t
+1
(9)
(
c
0
)
t
+2
=[(
x
0
)
t
+1
⊕
(
x
2
)
t
][(
x
0
)
t
+1
⊕
(
c
0
)
t
+1
]
⊕
(
x
0
)
t
+1
with
c
0
the carry bit of the FCSR. The previous equations correspond to the
description of the addition with carry at the bit-level (and represented by
in
the figures). This operator is also known as a full adder. The Equations corre-
sponding to time
t
+ 2 depend on the carry, (
c
0
)
t
+1
, generated at time
t
+1. This
dependency between full adders is a characteristic of a well-known arithmetic
circuit: the
n
-bit ripple carry adder (Figure 6(b)).
Thus, all the full adders in a
d
sub-sequences generator are replaced by
d
-bit
ripple carry adders as shown in Figure 7.
We can derive a more general representation of a multiple steps Galois FCSR
from the previous formula: