Biomedical Engineering Reference
In-Depth Information
{
}
m
[
]
( )
(
)
( )
∑
x
=
Ax
−
b
(
c
*
x
)
−
h
,
−
1
Θ
Φ
−
1
+
Re
Θ
I
+
Φ
Φ
−
1
+
i
Q
T
i
(18)
k
k
k
1
*
+
T
(
−
i
)
Θ
Φ
T
(
i
)
≥
0
where
n
x
∈
is the state vector;
A
×
n
n
∈
is a
constant matrix;
B
and
C
are matrices with
b
k
and
c
k
,
(20)
as columns;
n
h
∈
is a constant vector
and the nonlinear functions
k
=
1
m
hold and matrix
CQ
is symmetric, then
system (18) is dichotomic for all slope restricted
nonlinear functions satisfying (19). If additionally,
all equilibria are isolated, then each bounded
solution approaches an equilibrium point.
(
k
are differen-
tiable, slope restricted, bounded functions; the
matrix transfer function of the linear part of (18)
is
)
*
−
B
1
−
1
(
A
)
−=
, where the asterix denote
the transpose and complex conjugate. System
(18) includes neural networks (13) provided the
functions involved there have special forms that
are quite easy to deduce (
op. cit.
).
The study of the qualitative properties of (18)
has different approaches (Noldus
et al.
, 1994, 1995;
Danciu & Răsvan, 2000). We shall present here
the approach which places the problem within
the field of
The Theory of Systems with Several
Equilibria
(Danciu & Răsvan, 2000). Two cases
have to be considered
*
−
1
T
(
s
)
C
(
sI
A
)
B
b.
The case of the bounded nonlinearities
verifying
−
~
( )
≤
p
k
≤
p
(21)
k
k
Theorem 2.
Consider system (18) under the
assumptions of Theorem 1. Assume additionally
that it is minimally stable, the nonlinear functions
satisfy (21) and the equilibria are isolated. Then
each solution of (18) approaches asymptotically
an equilibrium state (the system (18) is gradi-
ent-like).
a.
The case of restricted slope nonlinearities
verifying
d
(
)
k
k
<
<
,
k
=
1
m
k
k
d
For systems with sector restricted nonlin-
earities, the required
minimal stability property
(notion introduced by V.M. Popov (1966, 1973)
means that in order to obtain stability for
all
nonlinear (and linear) functions from some sector,
it is (minimally) necessary to have this property
for
a single linear function
within this sector. In
our case system (18) has to be internally stable
for a linear function of the class: there exist the
numbers
(19)
k
Denote
Φ
=
diag
(
,...,
)
,
Φ
=
diag
(
,...,
)
,
1
m
1
m
(
)
,
Q
=
diag
q
,
,
q
Θ
=
diag
(
1
,
)
1
m
m
Theorem 1:
Consider system (18) under the
assumptions:
~
k
∈
(
,
)
such that
k
k
i)
det ≠
A
;
0
−
m
~
ii)
(
A, B
)
is a controllable pair and
is an
*
A
b
c
(
C
*
,
A
)
k
k
k
observable pair;
1
is a Hurwitz matrix (has all its eigenvalues in the
open complex left half plane, Re
s <
0).
Consider now the case of the Hopfield clas-
sification neural network (1984) described by
iii)
det
C
*
A
−
1
B
=
det
T
(
0
≠
0
If for
there exists the sets of param-
k
=
1
m
,
eters
k
q
such that the
frequency domain inequality of Popov
>
0
,
,
≥
0
>
0
≠
0
k
k
k






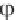





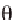















Search WWH ::

Custom Search