Environmental Engineering Reference
In-Depth Information
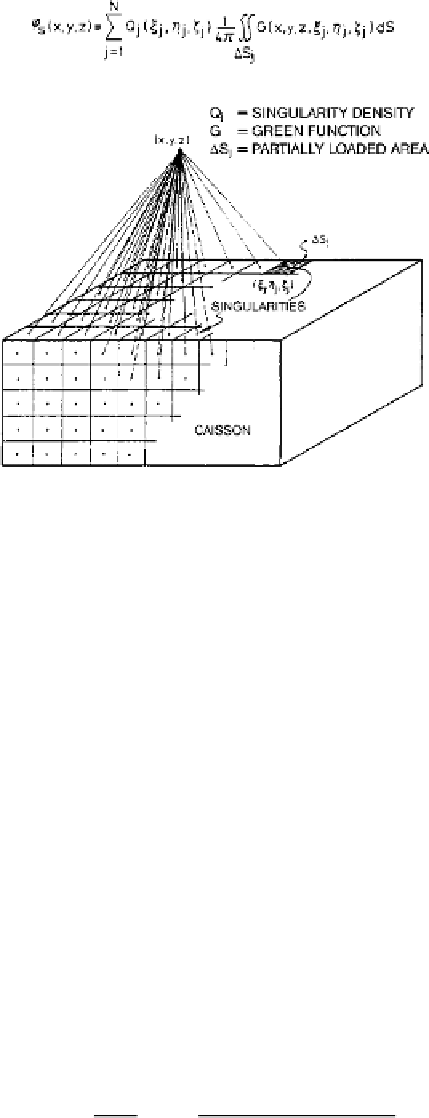
Fig. 2.36 Singularity distribution for a compact structure [30]
We therefore have a Fredholm integral equation of the second kind for determining the
singularity density Q (
j
,
h
,
z
) required. A closed solution to this equation is impossible
because the kernel
@
G
=@
n is very complex.
A numerical treatment requires us to divide the wetted surface of the body into a finite
number (N) of partially loaded areas (
D
S
j
) with singularities placed at their centroids
having a constant singularity density (Q
j
), see Figure 2.36.
The undisturbed wave potential (
F
0
) can be described with the linear approach of Airy,
but also with a non-linear approach, for example fifth-order Stokes. The perturbation
potential is basically described by a linear approach because satisfying the non-linear
surface condition is extremely difficult. Consequently, the total potential can satisfy
only the linearised boundary condition at the surface of the water [30].
The above integral equation can therefore be transformed into a set of linear equations
with the following form:
Q
i
þ
X
j
Q
j
¼
2
h
i
ð
;
j
¼
1
;
; ...;
Þ
a
ij
i
2
N
where
D
S
i
ZZ
@
Gx
i
;
y
i
;
z
i
; j
j
; h
j
; z
j
1
2
p
h
i
¼
@w
0
@
a
ij
¼
dS
j
and
@
n
n
D
S
j