Environmental Engineering Reference
In-Depth Information
Fig. 2.21 Superposition of primary wave and uniform
ow
The change in the wave height can be calculated with the help of the law of
conservation of energy and the above relationships as follows:
p
2
H
=
H
0
¼
= x
½
ð
1
þ x
Þ
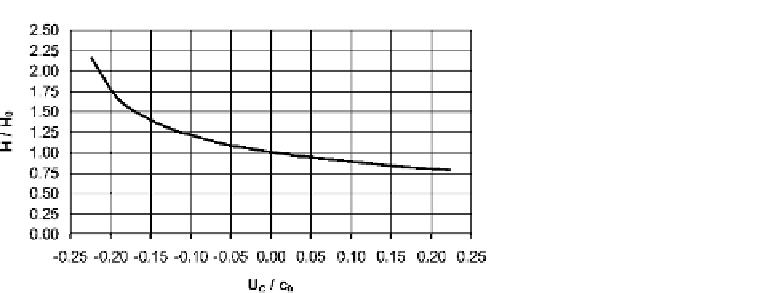
We can see from these equations that a current flowing in the direction of the wave (U
C
>
0)
causes the wavelength and the phase velocity to increase and the wave to flatten out. We get
the opposite effects when the current flows in the opposite direction to the wave
(Figure 2.21); U
C
/c
0
must be greater than
0.25 in this case. However, this limiting value
is not reached because the wave breaks first!
2.5.4 Waves of
nite steepness
The use of the harmonic primary wave, that is linear wave theory, is only justified for
the range of infinitesimal wave steepness, which in practical terms means H/
l<
1/50.
When designing nearshore structures in particular, we have to describe waves with a
finite steepness in a finite depth of water. To do this we need solutions to the non-linear
problem of the propagating gravity wave. As an explicit and complete solution to the
corresponding boundary value problems is impossible, we limit ourselves to approxi-
mate solutions of various orders.
The most important solutions to the non-linear wave problem are:
- Stokes waves,
- the elliptical (cnoidal) wave, and
- the solitary wave.
For an identical wave height, the wave crests of Stokes and elliptical waves are steeper
than those of Airy waves, the wave troughs flatter. The particle trajectories are no
longer closed, which means that transportation of mass takes place.
Stokes' wave theory makes use of formulations in the form of power series for the
profile and the velocity potential. So Stokes' third-order theory for deep water gives us
the following wave profile (see also Figure 2.22):