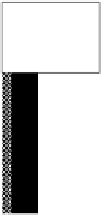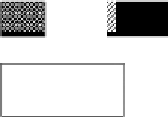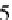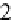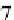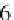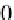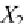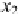Grayscale Implementation - Logic-based Nonlinear Image Processing - page 117

tor-based solutions is to construct a series of parallel detectors, one for each output
value. The amount of hardware required can be massive. It can be reduced by se-
quential testing, but this can be slow and result in non-deterministic processing
times.
An alternative approach is the bit-vector architecture. The concept is illustrated
by Handley through a simple example which is repeated here and in Fig. 8.12. The
function space is partitioned into a series of intervals taking the shape of disjoint
hyper-rectangles. In the two-variable case shown here, these correspond to simple
rectangles. Each interval has the same value of output associated with it. The num-
bers shown on each interval are labels (rather than output values). The intervals
with similar shading have the same output, therefore 2 and 5 have the same output
as do 1 and 6, and 0, 3, 4, and 7. The area outside of these intervals represents “no
operation.” Any single value of each variable will intersect a number of the inter-
vals. For example, in Fig. 8.12, the value of the variable x 1 shown intersects inter-
vals 2, 3, and 6. This is coded in a bit vector as (0, 0, 1, 1, 0, 0, 1, 0). Each interval 0
through 7 is represented (left to right) by a single bit. Each bit is 1 if the interval has
been intersected and 0 if it has not. Similarly, the value of the variable x 2 shown in-
tersects intervals 1 and 3. This is coded in a bit vector as (0, 1, 0, 1, 0, 0, 0, 0). To de-
termine the interval at location ( x 1 , x 2 ) the two bit vectors are simply ANDed together
to compute their intersection, which in this case is (0, 0, 0, 1, 0, 0, 0, 0), or interval 3.
It may be that the intersection forms the empty set in which case this is a “No opera-
Figure 8.12 Determination of intervals. The diagram shows a nonincreasing function of two
variables x 1 and x 2 . The space is partitioned into a series of hyper-rectangles each returning
a single value. A look-up table of bit vectors, indicating which intervals are intersected, is
pre-computed for each value of x 1 and x 2 . In the example above, the first variable x 1 returns a
bit vector of (0,0,1,1,0,0,1,0) representing intervals 2, 3, and 6. The second variable x 2 re -
turns a bit vector of (0,1,0,1,0,0,0,0) representing intervals 1 and 3. The intersection of these
bit vectors is (0,0,0,1,0,0,0,0) identifying the correct interval as 3.