Game Development Reference
In-Depth Information
Multiplying two unit quaternions is similar to multiplying two rotation matrices
together. The result represents the first orientation rotated by the second, and the
result is different depending on the order in which you perform the multiplication.
The big problem with quaternions is that they are almost impossible to visualize.
If given a set of Euler angles or an axis-angle pair, most people can form an image
in their mind of what that rotation would look like, but the same can't be said
of quaternions.
Quaternions can however be created fairly easily from both a rotation matrix
(and therefore Euler angles) and an axis-angle pair. The following diagram
shows the relationship between the axis-angle pairs and quaternions:
Quaternions really come into their own for 3D animation of boned characters, a topic
we will be coming to later in this chapter. This is a technique that requires an awful
lot of rotations to be calculated every time you want to update the animation frame,
and luckily quaternions make this far more efficient in terms of both memory usage
and execution speed.
While the theory behind quaternions may be a little scary for us mere mortals,
there is really little need to worry about the math, as Marmalade provides us
with a quaternion class,
CIwFQuat
, that we can use. As an example, creating a
quaternion from an axis-angle pair and then producing a rotation matrix from
it can be done as follows:
CIwFQuat lQuat;
lQuat.SetAxisAngle(1.0f, 0.0f, 0.0f, PI / 2.0f);
CIwFMat lMat(lQuat);
Animating by scaling
The scaling factor is normally stored either as a vector containing the required size in
the x, y, and z axes, or alternatively as a single scale value which is applied equally to
each axis. Often the latter is sufficient, as models tend to look odd when they are not
scaled uniformly in each axis.









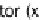

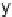










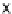
























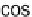









Search WWH ::

Custom Search