Simple Size and Shape Variables: Shape Coordinates - Geometric Morphometrics for Biologists - page 58

Centroid size is the square root of the summed squared distances of each landmark
from the centroid, giving a linearized measure of size (in a few very early publications, the
measure was not linearized). To compute centroid size, first compute the centroid (center)
of the form, whose location is the mean position of all coordinates. The mean is found by
simply averaging all the X -coordinates and all the Y -coordinates. For example, the three
landmarks of the triangle might be at (0, 0), (1, 0) and (0.3, 0.8) so the average X -coordinate
is the arithmetic mean of the three X -coordinates (0, 1, and 0.3), which is 0.433, and the
average Y -coordinate is the arithmetic mean of the three Y -coordinates (0, 0, 0.8), which is
0.267. Then calculate the squared distance of each landmark from the center, using the
standard formula for a squared distance between two points ( X 2 2 Y 1 ) 2 . This

sum gives a measure of size related to area; taking the square root gives the linearized
measure of size.
Size is thus measured separately from shape, and is geometrically independent of
shape. It is also statistically independent of shape (i.e. uncorrelated with shape, when the
landmarks vary independently and equally in all directions). This is a useful attribute of a
size measure because we do not want size to be intrinsically correlated with shape simply
by virtue of its formula. Rather, we want a measure of size that is correlated with shape
only when size and shape covary, that is, in the presence of allometry. Allometry is a com-
mon phenomenon, so we might expect that size and shape would usually be statistically
correlated. But that correlation is an empirical finding, not an outcome of the formula for
size. Centroid size, and other measures that are variants on centroid size, is the only size
variable that is statistically uncorrelated with shape in the absence of allometry . This is one
of the main reasons why centroid size is used as a size variable. The other reason is that
centroid size plays a crucial role in defining the metric for a distance between two shapes
(see Chapter 4).

X 1 ) 2

( Y 2 2

1

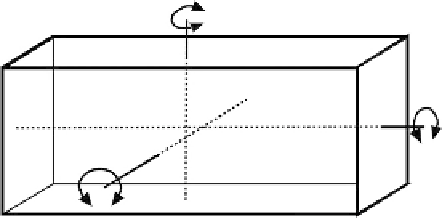
Bookstein Shape Coordinates in Three Dimensions
Shape coordinates for three-dimensional data can be calculated by an extension of the
formula for two-dimensional shape coordinates, but the formula is more complex because
three-dimensional objects can rotate around the three orthogonal axes, X , Y and Z
( Figure 3.8 ). The baseline is again translated, scaled to unit length oriented along the
X -axis and rotated so that the third landmark (C) is in the X , Y plane. Computing the

FIGURE 3.8 Rotation in 3D: axes of rotation.