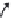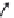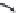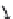Biology Reference
In-Depth Information
FIGURE 10.8
Landmarks sampled on the external body
form of piranhas.
4
3
5
2
6
14
15
7
1
16
8
13
12
11
10
9
Before doing this analysis, we remove the shape variance within each species that is
due to ontogeny, allowing us to estimate the shape of an average adult (this is done by
standardizing each species to its maximum adult size). Each species is represented by a
single data point, the mean shape for that species. There are nine species, so
N
9. The
5
result of the analysis is that
MD
0.00398. Of course, we cannot yet interpret this number
we cannot say if that value is large or small, or how uncertain it is. Before we can go any
farther, we need to deal with the issue of uncertainty.
To place confidence intervals on
MD
, we need first to consider the various parameters
being estimated. In general, there is uncertainty in the estimate of the mean shape of each
species, and in the estimate of the consensus. Both uncertainties must be taken into
account when computing confidence intervals. Additionally, when the mean shape of each
species is calculated by removing the variance due to ontogeny (or some other factor), we
must also account for the uncertainty of the regression model used to standardize the
shapes. We may also need to take a further source of uncertainty into account
the sam-
pling of species, because unless we have measured them all we must consider the uncer-
tainty of the grand mean that arises from our sampling of species. If we do not consider
this particular source of uncertainty, we cannot generalize from our sample of species to
the larger group that includes them, although we can make statements about our parti-
cular sample of species that takes the uncertainty of our sampling of them into account.
The confidence intervals might look odd because they frequently are not symmetric
about the mean, even when the distribution of shapes around the GLS consensus
is
sym-
metric. That symmetric distribution of shapes implies that the uncertainty in the estimate
of the mean is roughly equal in all directions (i.e. it is a hyperspherical solid). Turning to
the estimates of disparity, we can see why the uncertainty in the distance of a species from
grand mean is not symmetric about the mean distance even then. The hyperspherical
distribution of uncertainty in the mean yields a non-symmetric distribution of distances
there are many more possible locations of a species' mean that increase the distance than
there are that decrease it. As we can see in
Figure 10.9
, the line joining the grand mean to
a species' mean is in a single direction in a high dimensional space; random variation in
the position of the sample mean rarely lies along the line between the species' mean and
grand mean. In
Figure 10.9
,
D
is the distance from the species' mean to the grand mean
shape, and the circle around X represents the range of uncertainty about the species'
mean. The region within the circle that is a distance
D
or less from the grand mean is
shaded, and this region is clearly smaller than the unshaded region that is farther than
D
from the grand mean. This effect is even more pronounced in higher dimensions.
5