Information Technology Reference
In-Depth Information
Fig. 3.5
Transformation rules
a
−ₒ
1. In the first case, we assume that
s
ʔ
. Since
s
∼
t
, there exists some
ʘ
a
−ₒ
†
ʘ
.By(
3.22
), we get
ʘ
such that
t
ʘ
and
ʔ
∼
∈
[[
X
ʔ
]]
ˁ
∼
. It follows that
X
ʔ
]]
ˁ
∼
.
2. In the second case, we suppose
t
t
∈
[[
a
a
−ₒ
∈
ʘ
for any action
a
L
and distribution
a
−ₒ
†
ʘ
. Then by
s
∼
t
there exists some
ʔ
such that
s
ʔ
and
ʔ
∼
ʘ
.By
[[ [
a
]
s
(
3.22
), we get
ʘ
∈
[[
X
ʔ
]]
ˁ
∼
. As a consequence,
t
∈
−ₒ
ʔ
X
ʔ
]]
ˁ
∼
. Since
a
this holds for arbitrary action
a
, our desired result follows.
3.6.2.3
Characteristic Formulae
So far we know how to construct the characteristic equation system for a finitary
pLTS. As introduced in [
54
], the three transformation rules in Fig.
3.5
can be used to
obtain from an equation system
E
a formula whose interpretation coincides with the
interpretation of
X
1
in the greatest solution of
E
. The formula thus obtained from a
characteristic equation system is called a
characteristic formula
.
Theorem 3.10
Given a characteristic equation system E, there is a characteristic
formula ˕
s
such that ˁ
E
(
X
s
)
The above theorem, together with the results in Sect.
3.6.2.2
, gives rise to the
following corollary.
=
[[
˕
s
]]
for any state s.
Corollary 3.1
For each state s in a finitary pLTS, there is a characteristic formula
˕
s
such that s
∼
t iff t
∈
[[
˕
s
]]
.
3.7
Metric Characterisation
In the bisimulation game, probabilities are treated as labels since they are matched
only when they are identical. One might argue that this does not provide a robust
relation: Processes that differ with a very small probability, for instance, would be
considered just as different as processes that perform completely different actions.
This is particularly relevant to security systems where specifications can be given as

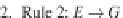
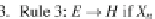
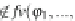













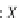


























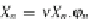



Search WWH ::

Custom Search