Information Technology Reference
In-Depth Information
Fig. 3.3
The network
N
(
ʔ
,
ʘ
,
R
)
f
(
s
,
t
) for all (
s
,
t
)
w
(
s
,
t
)
=
∈
R
and
w
(
s
,
t
)
=
0if(
s
,
t
)
∈
R
. We can check that
f
(
s
,
t
)
w
(
s
,
t
)
=
=
f
(
s
↥
,
s
)
=
ʔ
(
s
)
t
∈
S
t
∈
S
and similarly,
s
∈
S
w
(
s
,
t
)
=
ʘ
(
t
). So
w
is a weight function for (
ʔ
,
ʘ
) with respect
to
Since the lifting operation given in Definition
3.2
can also be stated in terms of
weight functions, we obtain the following characterisation using network flow.
R
.
†
ʘ if
Theorem 3.4
Let S be a finite set, ʔ
,
ʘ
∈
D
(
S
)
and
R
ↆ
S
×
S. Then ʔ
R
and only if the maximum flow in
N
(
ʔ
,
ʘ
,
R
)
is
1
.
Proof
The above property will play an important role in Sect.
3.8.2
to give an “on the
fly” algorithm for checking probabilistic bisimilarity.
Besides Theorems
3.1
and
3.4
, there are other equivalent ways of lifting relations.
Given a binary relation
Combine Theorem
3.1
(1) and Lemma
3.2
.
R
ↆ
×
ↆ
R
S
T
and a set
A
S
, we write
(
A
) for the set
{
∈
|∃
∈
R
}
R
R
ↆ
t
T
s
A
:
s
t
. A set
A
is
-closed if
(
A
)
A
.
Theorem 3.5
Let ʔ and ʘ be distributions over finite sets S and T , respectively.
†
ʘ if and only if ʔ
(
A
)
1. ʔ
R
≤
ʘ
(
R
(
A
))
for all A
ↆ
S.
†
ʘ if and only if ʔ
(
A
)
2. If
R
is a preorder, then ʔ
R
≤
ʘ
(
A
)
for each
R
-closed
set A
ↆ
S.
Proof




































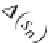















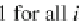





Search WWH ::

Custom Search