Information Technology Reference
In-Depth Information
1/2
1/2
˄
˄
˄
1/2
˄
1/2
˄
1/2
1/2
a
a
(a)
(b)
Fig. 6.1
The pLTSs of processes
Q
1
and
Q
2
. Reprinted from [
1
], with kind permission from
Springer Science+Business Media
a
−ₒ
a
with probability 1. However, the action [[
a.
0
]]
[[
0
]] cannot be simulated by a
˄
⃒
ˆ
a
−ₒ
corresponding move [[
Q
1
]]
. No matter which distribution
ʔ
we obtain from
executing a finite sequence of internal moves [[
Q
1
]]
˄
⃒
ʔ
, still part of it is unable
to subsequently perform the action
a
.
To address this problem, we propose a new relation
ʔ
⃒
ʘ
, to indicate that
ʘ
can be derived from
ʔ
by performing an unbounded sequence of internal moves; we
call
ʘ
a
weak derivative
of
ʔ
. For example [[
a.
0
]] will turn out to be a weak derivative
of [[
Q
1
]], that is, [[
Q
1
]]
⃒
[[
a.
0
]], via the infinite sequence of internal moves
˄
−ₒ
˄
−ₒ
˄
−ₒ
...
˄
˄
−ₒ
[[
Q
1
]]
[[
Q
1
2
↕
a.
0
]]
[[
Q
1
2
2
↕
a.
0
]]
−ₒ
[[
Q
1
2
n
↕
a.
0
]]
... .
Here, we make a significant use of “subdistributions” that sum to
no more than
one
[
2
,
3
]. For example, the empty subdistribution
ʵ
elegantly represents the chaotic
behaviour of processes that in communicating sequential processes (CSP) and in
must-testing semantics is tantamount to divergence, because we have
ʵ
ʱ
−ₒ
ʵ
for
any action
ʱ
, and a process like
rec
x.x
that diverges via an infinite
˄
path gives rise
to the weak transition
rec
x.x
⃒
ʵ
. So the process
Q
2
=
Q
1
2
↕
rec
x.x
illustrated
1
in Fig.
6.1
b will enable the weak transition [[
Q
2
]]
2
[[
a.
0
]], where intuitively
the latter is a proper subdistribution mapping the state
a.
0
to the probability
⃒
1
2
.
Our weak transition relation
can be regarded as an extension of the
weak
hyper-transition
from [
4
] to partial distributions; the latter, although defined in a
⃒


























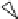




Search WWH ::

Custom Search