Environmental Engineering Reference
In-Depth Information
where subscript
k
denotes the degree of the polynomial π
k
()
, δ
jk
is the Kronecker symbol
equal to 1 when
j
=
k
and 0 otherwise, and
a
i
corresponds to the squared norm of π
j
()
:
2
def
def
(6.7)
a
i
=
π
()
i
=
π
()
i
,
π
()
i
.
j
j
j
i
i
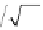
This family can be obtained by applying the Gram-Schmidt orthogonalization procedure
to the canonical family of monomials {1,
x
,
x
2
, …}. For standard distributions, the associated
family of orthogonal polynomials is well known. For instance, if
X
i
~ U(−1, 1) has a uniform
distribution over [−1, 1], the resulting family is that of the so-called
Legendre polynomials.
If
X
i
~ N(0, 1) has a standard normal distribution with a zero mean value and unit standard
deviation, the resulting family is that of
Hermite polynomials.
The families associated to
standard distributions are summarized in
Table 6.1
(Xiu and Karniadakis, 2002).
Note that the obtained family is usually not orthonormal. By enforcing the normalization,
an
orthonormal family
{
ψ
j
i
()
}
∞
0
is obtained from
Equations 6.6
and
6.7
by
j
=
ψπ
()
i
=
()
i
i
ai
=
1
…
,
,
Mj
,
∈
N
.
(6.8)
j
j
j
The normalizing coefficients are listed in
Table 6.1
for the standard families. For the sake
of illustration, Hermite polynomials up to degree 4 are plotted in
Figure 6.2
.
6.3.2.2 Multivariate polynomials
To build up a basis such as in
Equation 6.3
,
tensor products
of univariate orthonormal poly-
nomials are built up. For this purpose, let us define multi-indices (also called tuples) α ∈
M
that are ordered lists of integers
α = (α
1
, …, α
M
), α
i
∈
.
(6.9)
One can associate a multivariate polynomial Ψ
α
to any multi-index α by
M
∏
def
Ψ
α
()
x
=
ψ
()
i
( ,
x
(6.10)
α
i
i
i
=
1
Table 6.1
Classical families of orthogonal polynomials
Type of variable
Distribution
Orthogonal polynomials
Hilbertian basis
ψ
κ
(x)
Uniform
U
(
−
1, 1)
1
[
−
1,1]
(
x
)/2
Legendre
P
k
(
x
)
1
21
Px
k
()
k
+
1
2
Hermite
H
e
κ
()
x
Gaussian
N
(0, 1)
Hx k
e
k
()
!
π
e
x
−
2
2
Gamma
Γ
(
a
,
λ
=
1)
x
a
e
−
x
1
R
+
(
x
)
Laguerre
Lx
a
()
Γ++
1
(
ka
k
)
Lx
a
()
!
Beta
B
(
a , b
)
ab
,
ab
,
()
(
1
x x
Ba Bb
) ( )
()()
a
1
b
Jacobi
J
()
x
J
()
x
−
+
k
k
abk
,,
1
−
x
[
]
11
,
ab
kab
2
++
1
ka
1
(
kb
1
)
Γ(
++ ++
+++
)Γ
2
abk
=
,,
2
1
(
kab
1
)
(
k
1
)
+++
Γ
Γ
+

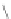
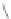














Search WWH ::

Custom Search