Environmental Engineering Reference
In-Depth Information
y
(m)
#6
#12
#18
#24
#30
11
#5
#11
#17
#23
#29
9
#4
#10
#16
#22
#28
7
#3
#9
#15
#21
#27
5
#2
#8
#14
#20
#26
3
#1
#7
#13
#19
#25
1
x
(m)
1
3
5
7
9
O
Figure 4.3
Location of the soil samples.
2
∆
Ω
ρ()
∆
=
exp
−
(4.8)
where Ω is the correlation distance and Δ is the distance between two points in the ran-
dom field.
In a stationary lognormal random field, the mean (μ), standard deviation (σ), and
the correlation distance (Ω) are the three parameters to be calibrated, that is, θ = {μ,
σ, Ω}. Suppose 30 samples (
n
= 30) are taken from the ground with locations shown
in
Figure 4.3.
The coordinates of the locations of the soil samples as well as the und-
convenience of presenting the likelihood function later, let λ
=
ln{
µ
/1
+
(
σµ
)}
2
and
ξ
=
ln[
1
+
(
σ µ
)],
2
where λ and ξ are the mean and standard deviation of ln(
c
u
),
respectively.
Let
c
ui
denote the
i
ith measured value of
c
u
. In this example,
d
i
= {
c
ui
}, and the observed
data can be denoted as
d
= {
d
1
,
d
2
, … ,
d
n
} = {
c
u
1
,
c
u
2
, … ,
c
u
n
}. Let Λ be an
n
-dimensional
column vector with all elements being λ and
T
be an
n
×
n
correlation matrix with
T
ij
being the correlation coefficient between ln(
c
u
) at location
i
and location
j
. Based on the
assumption of a lognormal random field, it can be shown that ln(
d)
follows the multivari-
ate normal distribution with a mean of Λ and a covariance matrix of ξ
2
T
(e.g., Fenton
1999). Based on the probability density function of a multivariate normal distribution,
the chance to observe
d
given θ, or the likelihood function of θ, can be written as (e.g.,
Fenton 1999):
1
(ln
dTd
−
Λ
)
T
−
1
(ln
−
Λ
)
(4.9)
l
(
θ
d
)
=
exp
−
(
2
πξ
22 12
)
n
||
T
2
ξ
2
where ln
d
is a vector with the
i
ith element being the logarithm of the
i
ith element of
d
.













































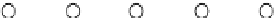












































































































































































































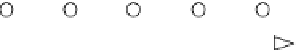


Search WWH ::

Custom Search